Z-ooM

红黑树的基本结构

红黑树(Red-black tree) 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，常用于关联数组、字典等。C++ 中的标准关联容器set、multiset、map、multimap内部采用的数据结构就是红黑树。

红黑树的定义：

每个节点只能是红色的或黑色的
根节点是黑色的
每个叶子节点都是黑色的
如果一个节点是红色的，那么它的孩子节点必须是黑色的
从任意一个节点到叶子节点经过的黑色节点个数是一样的

2-3 树

在介绍红黑树前先了解其等价形式 2-3 树，对后面理解红黑树的定义很有帮助。 2-3 树的定义：

满足二叉搜索树的性质
节点可以存放一个(2-节点)或两个(3-节点)关键字
每个节点有两个或三个孩子节点

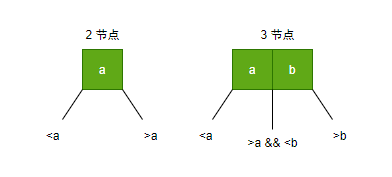
学过B-树的会发现其节点与B-树相似，类似三阶B-树。统样，2-3 树 的基本操作也与B-树类似。 2-3 树的基本操作：

插入： 插入新节点时，往叶子节点插入
分解： 4-节点可以被分解成 3 个 2-节点组成的树，且分解后树的根节点要向上与其原来的父节点融合。

下面按序列 {1,2,3,4,5} 构建一棵 2-3 树：

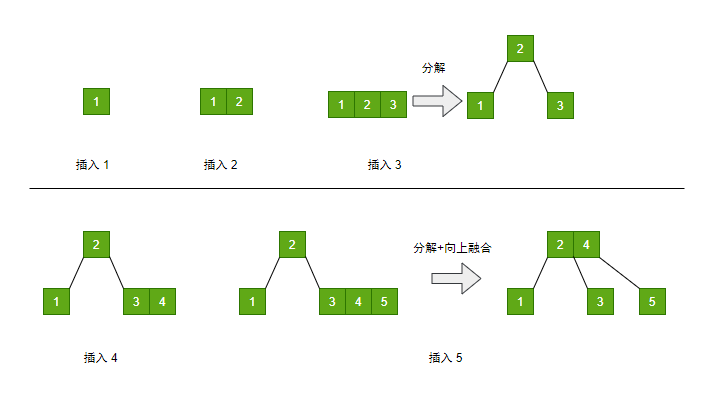
不难发现在上述操作中 2-3 树 始终能够保持严格的平衡。但是由于其节点关键字个数不唯一，且拆分合并操作的编程实现较复杂，因此我们希望通过添加一些规则，将其转化成二叉树，且转换后的二叉树仍然具有2-3树的自平衡优点，这就是红黑树。

2-3 树 -> 红黑树

对于 2-3 树 的两种结点，有不同的转换规则：

2-结点： 直接转换成红黑树的黑节点
3-节点： 拆开两个关键字，左关键字标红（表示红色节点与其父节点在2-3树中曾经是同级关系），右关键字标黑，右关键字作左关键字的父节点

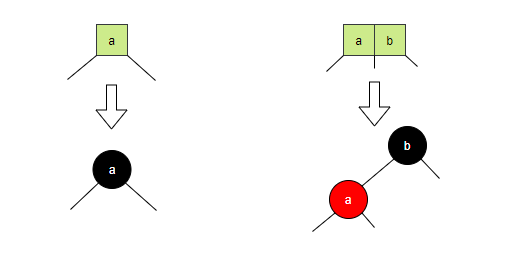
按照上述规则，我们将序列 {3,5,8,10,12,15,16,18,19,4,20} 构建的 2-3 树 转化为一棵红黑树：

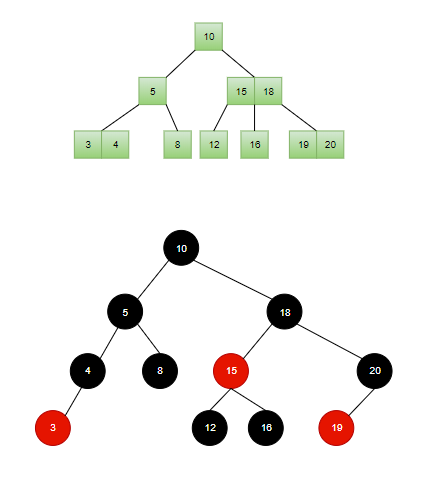
回顾一下红黑树的性质, 判断上图的树是否满足所有性质：

每个节点只能是红色的或黑色的
根节点是黑色的
每个叶子节点都是黑色的
如果一个节点是红色的，那么它的孩子节点必须是黑色的
从任意一个节点到叶子节点经过的黑色节点个数是一样的

可以发现除了第三个性质其余都满足了。事实上，性质三中说的叶子节点指的是为空的叶子节点，所以，完整的红黑树应为：

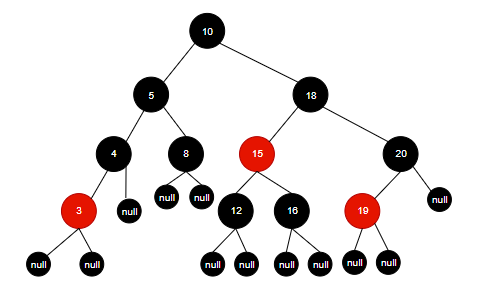
如此一来，便使得所有性质都满足了。

红黑树的创建

前面提到，创建 2-3 树 的代码编写较为复杂，因此我们肯定不会先创建一棵 2-3树 再将其转换成红黑树。因为我们可以很方便地创建一棵二叉树，红黑树不过是性质比普通二叉树多了些，因此在创建红黑树时只需在创建二叉树的方法的基础上多加几种操作来保证红黑树的性质不被破坏就行了。

插入： 由于前面提到2-3树的插入操作都发生在叶子节点，且都是先将待插入元素与该叶子节点融合。因此新插入节点和原位置的叶子节点为平级关系。又前面提到红色节点与其父节点曾是原级关系，故插入节点应为红色。 创建演示： 下图中红边所连接的子节点为我们说的红色节点（《算法第四版》的说法为红分支所连节点为红节点，类比着看，其实没差别因为一条分支只唯一对应一个结点）。

观察上述创建过程，发现当插入节点位于右分支时我们需要左旋操作，因为红色节点只能出现在左分支。

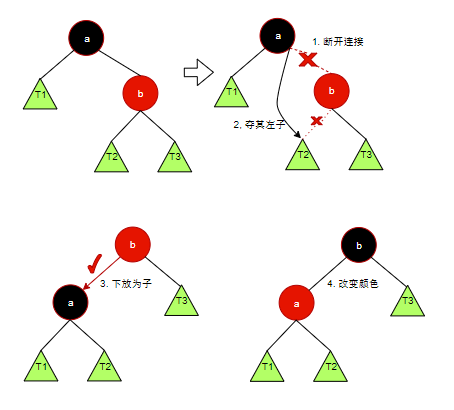
左旋操作的伪码实现：

RBNode* leftRotate(RBNode* node)
{
    RBNode *r_temp = node -> right;
    node -> right = r_temp -> left;
    r_temp -> left = node;
    r_temp -> color = node -> color;
    node -> color = RED;
    return r_temp;
}

右旋操作与左旋操作类似：

RBNode* rightRotate(RBNode* node)
{
    RBNode *l_temp = node -> left;
    node -> left = l_temp -> right;
    l_temp -> right = node;
    l_temp -> color = node -> color;
    node -> color = RED;
    return l_temp;
}

翻转颜色操作：

void flipColor(RBNode *node)
{
    node -> color = RED;
    node -> left -> color = BLACK;
    node -> right -> color = BLACK;
}

插入操作：

有了上述基本操作的实现基础，我们来研究插入操作的实现。插入按插入位置分三种情况：

插入操作的实现：

RBNode* insert(RBNode *&root, KeyType key, ValueType value)
{
  if(root == NULL)
    return new RBNode(key, value, 1, RED);// 插入节点为红色

  if(key < root->key)      root -> left  = insert(root->left, key, value);
  else if(key > root->key)   root -> right = insert(root->right, key, value);
        else                  root -> value = value;

  // 应对三种情况的操作
  if(isRed(root->left) && !isRed(root->left))   root = leftRotate(root);
  if(isRed(root->left) && isRed(root->left->left))  root = rightRotate(root);
  if(isRed(root->left) && isRed(root->right))   flipColor(root);

  root -> N = size(root->left) + size(root->right) + 1;
  return root;
}

整体代码

#include <bits/stdc++.h>

#define RED true
#define BLACK false
using namespace std;
#define KeyType int
#define ValueType string
class RBNode {

  friend bool isRed(RBNode *node);
  friend RBNode* leftRotate(RBNode *node);
  friend RBNode* rightRotate(RBNode *node);
  friend void flipColor(RBNode *node);
  friend RBNode* insert(RBNode *&root, KeyType key, ValueType value);
  friend int size(RBNode *node);
  friend RBNode* search(RBNode *root, KeyType key);

public:
  RBNode(KeyType k, ValueType v, int n, bool c) : key(k), value(v), N(n), color(c), left(NULL), right(NULL) { }

private:
  KeyType key;      // 节点保存的键值
  ValueType value;    // 键值关联的值
  RBNode *left, *right; // 左右孩子节点指针
  int N;          // 这棵子树中的节点数
  bool color;       // 节点颜色：真为红，假为黑
};

// 获得以node为根的树的节点数
int size(RBNode *node)
{
  if(node == NULL) return 0;
  return node -> N;
}

// 获得节点颜色
bool isRed(RBNode *node)
{
  if(node == NULL) return false;
  return node->color == RED;
}

// 改变节点颜色
void flipColor(RBNode *node)
{
  node -> color = RED;
  node -> left -> color = BLACK;
  node -> right -> color = BLACK;
}

// 左旋操作
RBNode* leftRotate(RBNode *node)
{
  RBNode *temp  = node -> right;
  node -> right = temp -> left;
  temp -> left  = node;
  temp -> color = node -> color;
  node -> color = RED;
  temp -> N     = node -> N;
  node -> N     = 1 + size(node->left) + size(node->right);
  return temp;  // 返回重置父节点指针
}

// 右旋操作
RBNode* rightRotate(RBNode *node)
{
  RBNode *temp  = node -> left;
  node -> left  = temp -> right;
  temp -> right = node;
  temp -> color = node -> color;
  node -> color = RED;
  temp -> N     = node -> N;
  node -> N     = 1 + size(node->left) + size(node->right);
  return temp;  // 返回重置父节点指针
}

RBNode* search(RBNode* root, KeyType key)
{
  if(root == NULL) return NULL;
  else
  {
    if(root -> key == key) return root;
    else if(root -> key < key)
    {
      return search(root -> left, key);
    }
    else
    {
      return search(root -> right, key);
    }
  }
}

RBNode* insert(RBNode *&root, KeyType key, ValueType value)
{
  if(root == NULL)
    return new RBNode(key, value, 1, RED);

  if(key < root->key)       root -> left  = insert(root->left, key, value);
  else if(key > root->key)  root -> right = insert(root->right, key, value);
  else                      root -> value = value;

  // 应对三种情况的操作
  if(isRed(root->left) && !isRed(root->left))       root = leftRotate(root);
  if(isRed(root->left) && isRed(root->left->left))  root = rightRotate(root);
  if(isRed(root->left) && isRed(root->right))              flipColor(root);

  root -> N = size(root->left) + size(root->right) + 1;
  return root;
}

至此本篇文章结束...

红黑树揭秘：深入探索自平衡的艺术

红黑树的基本结构

2-3 树

2-3 树 -> 红黑树

红黑树的创建

整体代码

评论