【Pytorch基础】卷积神经网络基础

回顾

 之前我们讨论的网络都是由线性层串起来组成的，其相邻层的任意两个结点之间都有一个链接（权重），因此称之为全连接神经网络(Fully Connected Nerual Network)。但是，在处理图像时，由于输入被reshape成一个$N \times 1$的向量，使得图像的二维特征被破坏，所以其并不能较好地用于图像问题。

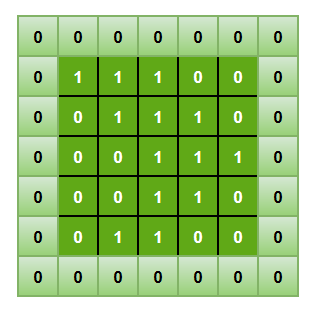
计算机眼中的图像

---

 毫无疑问，你可以很快分辨下图中的动物是只猫。但在计算机“眼中”，它仅仅是一个数字序列。图像由一个个像素组成，每一个像素通常以RGB(Red,Green,Blue)三原色（三通道）表示。但为了简化，我们使用灰度（0-255）表示，仅仅一个数字就可以表示（0：黑色 255：白色）。如此一来，对于一张$200\times 200$像素的图片，在计算机眼中就为一个$200\times 200$的矩阵。

卷积神经网络

基本操作：

1、卷积运算：

---

 顾名思义，卷积神经网络得名于“卷积”运算。在卷积神经网络中，卷积的主要目的是从目标图像中提取“特征”。通过使用输入数据中的小方块（矩阵分块）来学习图像特征，卷积运算保留了像素间的空间关系。
 正如前文所说，每个图像都可以被计算机看成是一个像素值矩阵。现仅考虑一个单通道的$1\times 5\times 5$像素的图像矩阵$W_{img}$：

再令一个$3\times 3$的矩阵$W_{f}$：

将$3\times 3$的矩阵在$5\times 5$矩阵上移动并将对应位的数值相乘并求和，得到一个新的矩阵即为卷积运算后的特征值矩阵：

多通道的卷积运算，下图输入图像为3通道，每一个通道都要配一个卷积核：

 这个由特征值组成的矩阵被称为 卷积特征 或 特征映射 。而上述参与卷积运算的$3\times 3$矩阵被称为 卷积滤波器 或 核 或 特征探测器 （以下统称滤波器，但是事实上过滤器的作用就是原始图像的 特征检测器）。上述例子中过滤器在图像矩阵上每次移动1个像素单位，称为 步幅 。

 不难发现，不同的滤波器作用于相同图像上会得到不同的特征映射，下图列出了一些滤波器的取值以及功能作用(边缘检测，锐化等)：

 总的来说，一个滤波器在输入图像上移动（卷积操作）以生成特征映射。在同一张图像上，另一个滤波器的卷积生成了不同的特征图。需要注意到，卷积操作捕获原始图像中的局部依赖关系很重要。还要注意这两个不同的滤波器如何从同一张原始图像得到不同的特征图。请记住，以上图像和两个滤波器只是数值矩阵。
 实际上，卷积神经网络在训练过程中会自己学习这些滤波器的值（尽管在训练过程之前我们仍需要指定诸如滤波器数目、大小，网络框架等参数）。我们拥有的滤波器数目越多，提取的图像特征就越多，我们的网络在识别新图像时效果就会越好。

特征映射（卷积特征）的大小由我们在执行卷积步骤之前需要决定的三个参数控制：

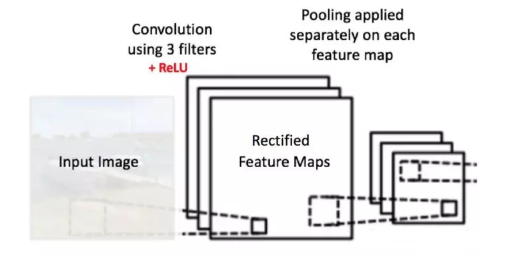
• 深度：深度对应于我们用于卷积运算的过滤器数量。在图6所示的网络中，我们使用三个不同的过滤器对初始的船图像进行卷积，从而生成三个不同的特征图。可以将这三个特征地图视为堆叠的二维矩阵，因此，特征映射的“深度”为3。

• 步幅：步幅是我们在输入矩阵上移动一次过滤器矩阵的像素数量。当步幅为1时，我们一次将过滤器移动1个像素。当步幅为2时，过滤器每次移动2个像素。步幅越大，生成的特征映射越小。
• 零填充：有时，将输入矩阵边界用零来填充会很方便，这样我们可以将过滤器应用于输入图像矩阵的边界元素。零填充一个很好的特性是它允许我们控制特征映射的大小，如果不做填充，若卷积核为$n\times n$则卷积运算后图片长宽减少$n/2$。添加零填充也称为宽卷积，而不使用零填充是为窄卷积。

2、非线性操作（ReLU操作）

---

 每次卷积操作之后，都会进行一次ReLU操作，其全称为修正线性单元（Rectified Linear Unit),是一种非线性操作。以下为修正线性函数的图像及表达式：

$$f(x)=\begin{cases} 0, & x<0 \\\\ x, & otherwise \end{cases}$$

 ReLU 是一个针对元素的操作（应用于每个像素），并将特征映射中的所有负像素值替换为零。ReLU 的目的是在卷积神经网络中引入非线性因素，因为在实际生活中我们想要用神经网络学习的数据大多数都是非线性的（卷积是一个线性运算 —— 按元素进行矩阵乘法和加法，所以我们希望通过引入 ReLU 这样的非线性函数来解决非线性问题）。
从可以很清楚地理解 ReLU 操作。它展示了将 ReLU 作用于某个特征映射得到的结果。这里的输出特征映射也被称为“修正”特征映射。

其他非线性函数如 Sigmoid 或 tanh 也能达到类似效果，但是 ReLU 函数的效果是最好的。

3、池化（Pooling）

---

 空间池化（也称为子采样或下采样）可降低每个特征映射的维度，并保留最重要的信息。空间池化有几种不同的方式：最大值，平均值，求和等。

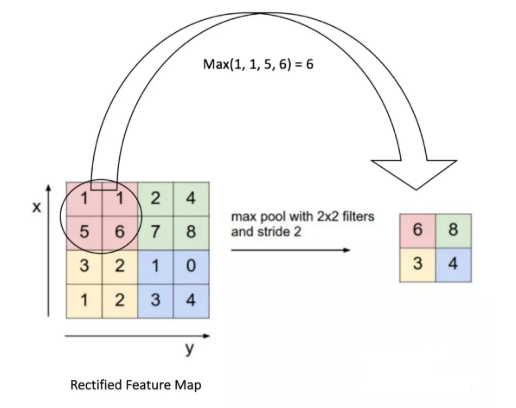
 在最大池化的情况下，我们定义一个空间邻域（例如一个2 × 2窗口），并取修正特征映射在该窗口内最大的元素。当然我们也可以取该窗口内所有元素的平均值（平均池化）或所有元素的总和。在实际运用中，最大池化 的表现更好。
 下图展示了通过2 × 2窗口在修正特征映射（卷积+ ReLU 操作后得到）上应用最大池化操作的示例:

 我们将2 x 2窗口移动2个单元格（也称为“步幅”），并取每个区域中的最大值。如图9所示，这样就降低了特征映射的维度,变成了一个$2\times 2$的矩阵。
 由于池化操作分别应用于每个特征映射（因此，我们从三个输入映射中得到了三个输出映射）。

两种池化方法的结果对比：

 池化的作用是逐步减少输入的空间大小。具体来说有以下四点：

• 使输入（特征维度）更小，更易于管理
• 减少网络中的参数和运算次数，因此可以控制过拟合
• 使网络对输入图像微小的变换、失真和平移更加稳健（输入图片小幅度的失真不会改池化的输出结果 —— 因为我们取了邻域的最大值/平均值）
• 可以得到尺度几乎不变的图像（确切的术语是“等变”）。这是非常有用的，这样无论图片中的物体位于何处，我们都可以检测到

 目前为止，我们已经了解了卷积神经网络中 卷积、ReLU、池化 的工作原理。

Pytorch构建卷积神经网络

---

 如下图所示的卷积神经网络，左侧部分负责图像的特征提取，之后就是一个全连接网络完成最后的分类操作。

 卷积神经网络的构建，简单来说就是上述基本操作的组合。先不谈网络的性能如何，要想网络能够正常工作，必须理清楚层与层之间的输入出入的维度关系。使得数据能够正常传递。

卷积层的构造

输入通道为N，输出通道为1的卷积层

可见，卷积核的大小与输入没啥关系，但是卷积核的通道数必须与输入的通道数一致。

输入通道为N，输出通道为M的卷积层

上图所示，每个卷积核对输入进行多通道卷积运算后输出一个特征映射（FeatureMap）,m 个卷积核生成m个特征映射，最终将它们拼接起来输出一个m通道的。可见，每一个卷积核的通道数量与输入通道数一致，且卷积核数量m决定了输出的通道数。

总结试验

 由上文可知，已知输入维度为$(n\times width{in} \times height{in})$和想要的到的输出维度$(m\times width{out} \times height{out})$我们就可以计算得出需要$m$个维度为$(n\times kernelsize{width} \times kernelsize{height})$的卷积核，即一个4维的张量（Tensor）。

import torch
in_channels, out_channels = 5,10 # 输入通道与输出通道
width, height = 100, 100 # 输入的宽高大小
kernel_size = 3 # 卷积核大小为3*3
batch_size = 1 # 再次强调torch中的训练输入都以一个minibatch为单元，故必须定义batch_size

inputs = torch.randn(batch_size,in_channels,width,height) # 从正态分布采样，生成一个输入

conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size=kernel_size) # 定义一个卷积层（输入通道数，输出通道数，卷积核大小（可为元组(3,5)等））

output = conv_layer(inputs) # 前馈计算

print(inputs.shape) # 输入维度（个数（batch_size），通道，长，宽）
print(output.shape) # 输出维度 （个数，通道，长，宽）
print(conv_layer.weight.shape) # 卷积核维度

输出:

torch.Size([1, 5, 100, 100])
torch.Size([1, 10, 98, 98])
torch.Size([10, 5, 3, 3])

Padding 和 步幅设置 操作实例

 Padding操作用来控制输出图像的大小（长宽）,若卷积核大小为$n\times n$则要维持输入大小与输出一致要padding $n/2$ 圈的0.

# 输入
inputs = [3,4,5,6,7,
          4,5,6,7,8,
          1,2,3,4,5,
          4,2,6,5,7,
          2,4,6,9,4]
inputs1 = torch.Tensor(inputs).view(1,1,5,5) # 转为神经网络允许的输入维度的tensor
inputs2 = torch.Tensor(inputs).view(1,1,5,5)

conv_layer1 = torch.nn.Conv2d(1,1,kernel_size=3,padding=1,bias=False) # padding=1,会给输入填充一圈0，不添加偏置量
conv_layer2 = torch.nn.Conv2d(1,1,kernel_size=3,stride=2,bias=False) # 设置步幅为2

kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1,1,3,3) # 卷积核权重张量

conv_layer1.weight.data = kernel.data # 初始化卷积核的权重
conv_layer2.weight.data = kernel.data

output1 = conv_layer1(inputs1) # 前馈计算
output2 = conv_layer2(inputs2)

print(output1)
print(output2)

输出：

tensor([[[[116., 184., 223., 262., 172.],
          [ 94., 153., 198., 243., 156.],
          [ 90., 162., 192., 251., 155.],
          [ 92., 176., 245., 267., 164.],
          [ 48.,  90., 129., 130.,  75.]]]],
       grad_fn=<MkldnnConvolutionBackward>)
tensor([[[[153., 243.],
          [176., 267.]]]], grad_fn=<MkldnnConvolutionBackward>)

ReLU 非线性变换

 采用torch.nn.function 类内置的relu函数。

池化操作实例（MaxPooling）

 采用默认的MaxPooling（2*2）, 其默认步幅（stride）为2。

# 输入
inputs = [3,4,5,6,7,
          4,5,6,7,8,
          1,2,3,4,5,
          4,2,6,5,7,
          2,4,6,9,4]
inputs = torch.Tensor(inputs).view(1,1,5,5)

maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2) # 池化层,大小为2，步幅默认为2

output = maxpooling_layer(inputs)

print(output)

输出：

tensor([[[[5., 7.],
          [4., 6.]]]])

用卷积神经网络实现MNIST手写数字识别

---

实现

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

batch_size = 64

# 对数据的处理：神经网络希望输入的数据最好比较小，最好处于（-1,1）内，最好符合正态分布。
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307, ),(0.3081, ))
])

# 训练集
train_dataset = datasets.MNIST(root='./dataset/mnist/',train=True,download=True,transform=transform)
train_loader = DataLoader(train_dataset,shuffle=True,batch_size=batch_size)

# 测试集
test_dataset = datasets.MNIST(root='./dataset/mnist/',train=False,download=True,transform=transform)
test_loader = DataLoader(test_dataset,shuffle=False,batch_size=batch_size)

# 模型类
class Net(torch.nn.Module):
    def __init__(self):
        super(Net,self).__init__()
        self.conv1 = torch.nn.Conv2d(1,10,kernel_size=5) # 卷积层1
        self.conv2 = torch.nn.Conv2d(10,20,kernel_size=5)# 卷积层2
        self.linear3 = torch.nn.Linear(320,10) # 全连接层3
        self.pooling = torch.nn.MaxPool2d(2) # 池化层
        
        
    def forward(self,x):
        # x (batch_size,channel,width,height)
        batch_size = x.size(0) # minibatch样本数量
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        x = x.view(batch_size,-1) # 转为全连接层允许的输入格式
        return self.linear3(x) # 后面要用softmax，故最后一层不做relu激活
    
model = Net()

# 损失函数和优化器
criterion = torch.nn.CrossEntropyLoss() # 交叉熵损失
optimizer = optim.SGD(model.parameters(),lr=0.01,momentum=0.5) # 随机梯度下降，带冲量

e_list = []
l_list = []
running_loss = 0.0
# 单轮训练的函数
def train(epoch):
    running_loss = 0.0
    Loss = 0.0
    for batch_idx, data in enumerate(train_loader,0):
        inputs, target = data
        optimizer.zero_grad()
        
        # 前馈计算
        outputs = model(inputs)
        # 损失计算
        loss = criterion(outputs,target)
        # 反馈计算
        loss.backward()
        optimizer.step()
        
        running_loss += loss.item() # 累加损失
        Loss += loss.item()
        # 每300次迭代（minibatch）训练更新,计算一次平均损失
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0
    e_list.append(epoch)
    l_list.append(running_loss/300)
    
def test():
    correct = 0 # 预测正确数
    total = 0 # 总样本数
    with torch.no_grad(): # 声明不计算梯度
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1) # 按列找最大值的下标，返回两个：最大值，下标
            total += labels.size(0) # labels矩阵的行数
            correct += (predicted == labels).sum().item() # 相等为1，否则为0
        print('Accuracy on test set: %d %%' % (100 * correct / total))
            
            
# 训练
if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

收敛图像：

• 参考：
• 《Pytorch深度学习实践》