【Pytorch基础】逻辑回归

机器学习 评论

回顾

 之前我们讨论过一个线性模型：

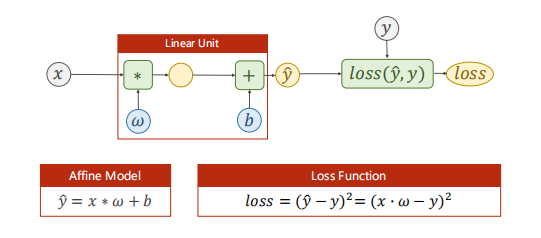
 上述模型预测出的$\hat{y} \in R$属于一个连续的空间内，我们称这类任务为回归任务。但是很多的机器学习任务要求我们去分类，比如给动物图片分类、给手写数字分类。对于分类任务，它预测出来的结果属于一个离散的集合，例如手写数字分类的结果集合为$y \in \left[ 0,1,2,3,4,5,6,7,8,9 \right]$。对于分类任务，用回归模型去预测是不合适的，因为这些类别之间并没有连续空间中的数值大小的含义（不能说某个类别大于或小于某个类别如猫大于狗）。在分类问题中，分类模型输出一个概率分布，再在所有类别的概率值（0 ~ 1）中找到最大值就是预测结果了。另外要注意的是，逻辑回归不是回归，它常用于分类问题，只是名字易让人误会。

 接下来，不妨用一个二分类任务来进行讨论。问题描述为每周学习时间与是否通过期末考试的关系。

输出映射

由于输出的是一个概率分布，每个类别的输出概率值都应该在0和1之间。因此，不能直接使用输出层的输出值。一方面因为输出层的输出值范围不确定，我们难以直观上判断这些值的意义；另一方面，由于真实标签是离散值，这些离散值与不确定范围的输出值之间的误差难以衡量。所以，需要将输出值映射到0和1之间。这里我们用到了 Logistic 函数，他是Sigmoid函数的一种:

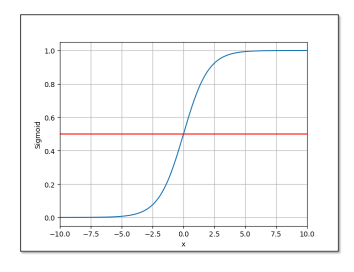
函数的预测输出变为：

还有其他的Sigmoid函数：

事实上，只要某函数满足单调增、有极限、为饱和函数（在超过一定阈值之后函数值变化微小）

损失函数

 对于线性模型的损失函数：

是计算预测值与真实值的差别的函数，是有实际意义的。但是，在分类问题中的输出为一个概率分布，不再是简单的几何1度量之间的差别，因此该损失函数不再适用。转而用计算两个分布之间差异的函数，其中交叉熵损失函数事一个常用的方法：

由于在上式中，向量$y^{(i)}$只有一个元素为 1 其余全为 0，于是该式即为：$Loss(\hat{y}^{(i)}, y^{(i)}) = -\log \hat{y}_{j=nozero}^{(i)}$。也就是说，交叉熵值关心对正确类别的预测概率，因为只要其值足够大，就可以确保分类结果的正确性。当然，遇到一个样本有多个标签时，例如一张图片中既有猫也有狗时，我们并不能做这一步简化。

参数释义：

  • $\hat{y}^{(i)}$ 是一个预测概率分布向量
  • $\hat{y}_{j}^{(i)} \Leftrightarrow P(Class_j)$
  • $y^{(i)}$ 一个维度为类别数且只有一个 1 其余为 0 的分布向量
  • $y^{(i)}_{j}$ 是向量 $y^{(i)}$ 中非 0 即 1 的元素
  • $q$ 为类别数量

对于一个二分类问题，损失函数为(BCE)：

参数释义：

  • $\hat{y} \Leftrightarrow P(Class_i)$
  • $y \Leftrightarrow (0 \text{ } or \text{ } 1)$

小批量的二分类损失函数为：

损失计算实例

逻辑回归模型的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# import torch.nn.functional as F
import torch

# 数据准备
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0],[0],[1]])

# 模型类实现
class LogisticRegressionModel(torch.nn.Module):
    def __init__(self):
        super(LogisticRegressionModel,self).__init__()
        self.linear = torch.nn.Linear(1,1)
        
    def forward(self, x):
        y_pred = torch.sigmoid(self.linear(x))
        return y_pred
    
model = LogisticRegressionModel()

# 损失函数和优化器
criterion = torch.nn.BCELoss(reduction="mean") # 二分类交叉熵损失函数
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

# 模型训练
w_list = []
loss_list = []
for epoch in range(10001):
    y_pred = model(x_data) # 计算预测值
    loss = criterion(y_pred,y_data) # 计算损失值（标量对象）
    print(epoch,loss) # 打印loss对象会自动调用loss.__str__(),就不会产生一个计算图
    
    w_list.append(model.linear.weight.item())
    loss_list.append(float(loss))
    
    optimizer.zero_grad() # 梯度归零
    loss.backward() # 反向传播
    optimizer.step() # 更新参数

# 训练后的参数值
print('w = ',model.linear.weight.item())
print('b = ',model.linear.bias.item())
# 训练后预测
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ',y_test.data.item())

收敛图像

1
2
3
4
5
6
import matplotlib.pyplot as plt

plt.plot(w_list, loss_list)
plt.ylabel('cost')
plt.xlabel('W')
plt.show()

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import numpy as np

# 测试数据集
x = np.linspace(0,10,200) # 0 到 10 之间采集200个点
x_t = torch.Tensor(x).view((200,1)) # 变成 200 * 1 的矩阵
y_t = model(x_t) # 前馈计算
y = y_t.data.numpy() # 拿到预测值数组

# 绘制0到10小时的通过情况
plt.plot(x,y)
plt.plot([0,10],[0.5,0.5],c='r')
plt.xlabel('Hours')
plt.ylabel('Probability of Pass')
plt.grid()
plt.show()

观察图像发现，在通过与不同边缘的大概在2.5个小时左右。

林深时见鹿Java 后端开发

栖迟於一丘