【Pytorch基础】Pytorch实现线性模型

回顾

 之前我们用纯python实现了一个线性模型。现在，以第一篇文章的例子来，试着用 Pytorch 提供的工具来实现一个线性模型。

Pytorch 写神经网络的套路

• 准备数据集
• 设计模型类（用来计算 $\hat{y}$）
• 构造损失函数和优化器（optmizer）
• 训练模型：
  • 前馈计算Loss
  • 反向传播Loss （梯度下降算法）
  • 更新

开始

1.准备数据集：

 在pytorch中，采用的是小批量地图下降算法，因此，$X$ 和 $\hat{Y}$ 是一个多维的 Tensor. 展开后的模型为：

$$\begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \hat{y}_3 \\ \dots \\ \end{bmatrix} = w \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \dots \\ \end{bmatrix} + b$$

上式的” $\cdot$ “ 表示的是数乘，要与矩阵乘法 “ $\times$ “ 区分开来。$w \cdot \begin{bmatrix} x_1 \ x_2 \ x_3 \ \dots \ \end{bmatrix}$会触发广播机制:

$$w \Rightarrow \begin{bmatrix} w \\ w \\ w \\ \dots \\ \end{bmatrix}$$

import torch as th
x_data = th.Tensor([[1.0],[2.0],[3.0]]) # 3 * 1 矩阵
y_data = th.Tensor([[2.0],[4.0],[6.0]])

2. 定义模型类：

 模型类中 init 函数与 forward 函数时必须实现的。反而 backward 函数无需定义，因为torch会根据计算图自动计算梯度。但是如果你认为默认的梯度计算性能不佳可以自己对torch内的Function类中实现的反向传播功能进行重载。

class LinearModel(th.nn.Module): # 必须继承自torch自带的模型基类nn.Module （nn == neural netword）
    def __init__(self): # 构造函数
        super(LinearModel, self).__init__() # 调用父类的构造函数
        self.linear = th.nn.Linear(1,1) # 构造一个th.nn.Linear 类（同样继承自Module,是内置的线性单元Linear Unit）的对象，该类包含了权重和偏置两个Tensor
        
    def forward(self, x): # 重载模型函数，必须要叫 forward, 用于前馈计算
        y_pred = self.linear(x) # linear 为一个可调用callable对象，他在类内实现了 __call__(self, *args, **kwargs) 函数， 实现前馈计算
        return y_pred
    
model = LinearModel() # 创建实例，model 也是一个可调用对象

model 对象大致结构如下：

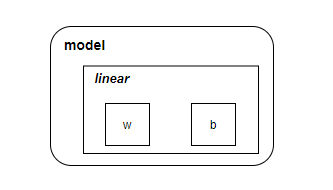
文档：

• torch.nn.Linear

3. 构造损失函数和优化器：

 当我们计算得到预测值 $\begin{bmatrix} \hat{y}_1 \ \hat{y}_2 \ \hat{y}_3 \ \dots \ \end{bmatrix}$ 后, 根据$Loss = (\hat{Y}- Y)^2$得损失为：

$$\begin{bmatrix} loss_1 \\ loss_2 \\ loss_3 \\ \dots \\ \end{bmatrix} = \left( \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \hat{y}_3 \\ \dots \\ \end{bmatrix} - \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \dots \\ \end{bmatrix} \right) ** 2 ,\text{（点方）}$$

又因为之后必须对Loss求导，故Loss值不能是一个矩阵向量，要将其内所有元素进行累加求和求均值成为一个标量:

$$Loss = \frac{1}{N} \sum \left( \begin{bmatrix} loss_1 \\ loss_2 \\ loss_3 \\ \dots \\ \end{bmatrix} \right)$$

# 构造损失函数和优化器
# 损失函数用MSELoss类（继承自Module），得到一个损失向量，需要再求和取平均（这里不求均值）得到Loss标量值
criterion = th.nn.MSELoss(reduction='sum') 
# 随机梯度下降算法，实例化SGD类，其中model.paramenters 会调用 model.linear.paramaters 来告诉优化器应该调整的权重；lr 为学习率
optimizer = th.optim.SGD(model.parameters(), lr = 0.01) 

Pytorch中其他的优化器：

• torch.optim.Adagrad
• torch.optim.Adam
• torch.optim.Adamax
• torch.optim.ASGD
• torch.optim.LBFGS
• torch.optim.RMSprop
• torch.optim.Rprop

文档：

• torch.nn.MSELoss
• torch.optim.SGD

4. 模型训练：

w_list = []
loss_list = []
for epoch in range(1000):
    y_pred = model(x_data) # 计算预测值
    loss = criterion(y_pred,y_data) # 计算损失值（标量对象）
    print(epoch,loss) # 打印loss对象会自动调用loss.__str__(),就不会产生一个计算图
    
    w_list.append(model.linear.weight.item())
    loss_list.append(float(loss))
    
    optimizer.zero_grad() # 梯度归零
    loss.backward() # 反向传播
    optimizer.step() # 更新参数

# 训练后的参数值
print('w = ',model.linear.weight.item())
print('b = ',model.linear.bias.item())
# 训练后预测
x_test = th.Tensor([[4.0]])
y_test = model(x_test)
print('y_pred = ',y_test.data.item())

最终预测：

w =  1.9994629621505737
b =  0.0012208453845232725
y_pred =  7.999072551727295

5. 打印查看收敛过程：

import matplotlib.pyplot as plt

# 绘图(权重与平均损失的关系)
plt.plot(w_list, loss_list)
plt.ylabel('cost')
plt.xlabel('W')
plt.show()