【Pytorch基础】梯度下降算法

回顾

 上偏文章我们尝试用枚举法找到权重的最优取值，并限定区间为0到4.1，步长为0.1,显然我们很快就能找到最优的权重。这是因为未知权重只有一个，复杂度为线性的。但如果模型为$y = f(w_1,w_2,w_3…,w_n,x)$, 有多个未知权重，如此一来即使你知道每个权重的取值在$[a,b]$内，枚举的时间复杂度也是$O((b-a)^n)$级别的。复杂度随权重数量指数级增长，这当然是不可接受的。

---

梯度下降

 已知平均损失函数为：

$$cost(w) = \frac{\sum_{i=0}^{n}(\hat y_i - y_i)^2}{n}$$

假设其图像为：

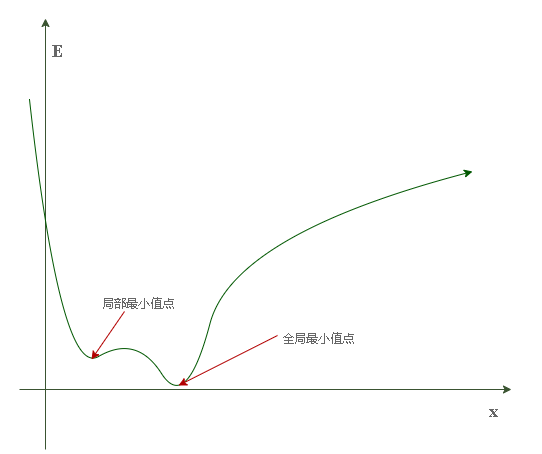
又假设当前权重位于红点位置：

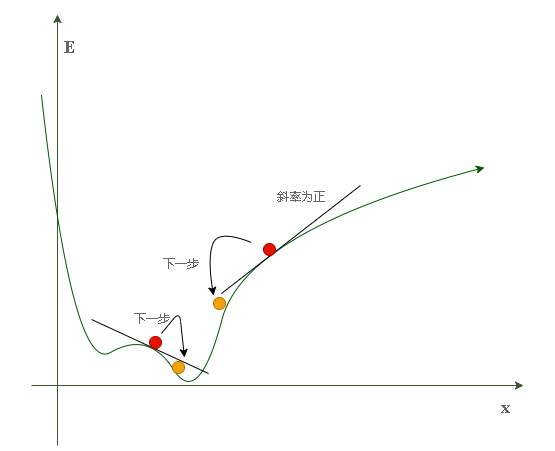
不难发现，当权重值(图中x)位于左侧红点（斜率为负）位置时，它应该往右（+）以靠近最优值；当权重值位于右侧红点（斜率为正）位置时，它应该往左（-）以靠近最优值。因此当前权重点的斜率方向可以规定其调整方向，而不必再去暴力枚举，调整方式为：

$$w = w - \alpha \frac{\partial cost}{\partial w}$$

也即：

• 当梯度(导数)为正时权重减少
• 增加的绝对值大小取决于 $\alpha$ , 称为学习率（一般来说取小一点好）

如此一来，每一次权重的迭代都朝着当前损失下降最快的方向更新，就称为梯度下降，是赤裸裸的贪心思想。按照我们对贪心算法的认知来看，当损失函数如上图所示为一个非凸函数时，其不一定每次都得到最优解，如它可能陷入如下情况中：

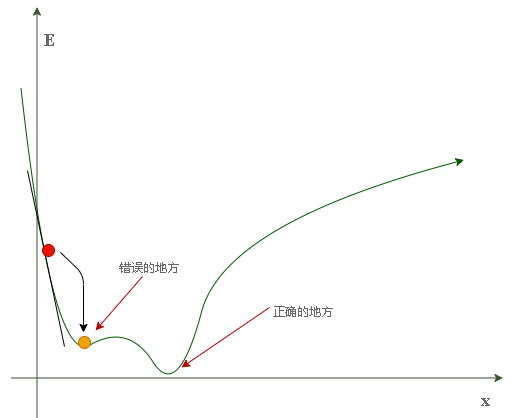
上图所示情况由于学习率很小而算法只顾眼前导致只能收敛于一个局部最优解，而与全局最优解失之交臂。
但是，实际应用中出现很多局部最优点的数量其实不会很多，反而会出现鞍点导致权重停止更新。

因为在鞍点处梯度为0，导致$\alpha \frac{\partial cost}{\partial w}$为0，权重无法继续迭代更新。

---

梯度下降算法

 接下来我们摈弃暴力枚举算法用梯度下降算法来对上篇文章例子中的权重进行更新。
首先求梯度函数：

$$\frac{\partial cost}{\partial w} = \frac{\partial}{\partial w} \left( \frac{\sum_{i=1}^{n}(\hat y_i - y_i)^2}{n} \right)$$ $$= \frac{1}{n}\sum_{i=1}^{n}(x_i \cdot w - y_i)^2$$ $$= \frac{1}{n}\sum_{i=1}^{n}2\cdot (x_i \cdot w - y_i)\frac{\partial (x_i \cdot w - y_i)}{\partial w}$$ $$= \frac{1}{n}\sum_{i=1}^{n}2\cdot x_i \cdot (x_i \cdot w - y_i)$$

因此，权重更新函数为：

$$w = w - \alpha \cdot \frac{1}{n} \sum_{i=1}^{n} 2 \cdot x_i \cdot (x_i \cdot w - y_i)$$

梯度下降算法具体实现

import numpy as np
import matplotlib.pyplot as plt

# 准备数据集
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

# 初始化权重w, 学习率 a
w = 0.1
a = 0.01

# 定义模型函数
def forward(x):
    return x * w;

# 定义平均损失函数
def cost(xs, ys):
    loss = 0 #损失和
    for x, y in zip(xs,ys):
        y_predict = forward(x)
        loss += (y - y_predict) ** 2
    return loss / len(xs)

# 定义梯度函数
def gradient(xs, ys):
    grad = 0 # 初始化梯度
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

print('训练前预测：',4,forward(4))

# 用于绘制损失函数
w_list = []
cost_list = []

# 开始训练模型16个世代
for epoch in range(100):
    cost_val = cost(x_data, y_data)
    grad_val = gradient(x_data, y_data)
    w -= a * grad_val
    w_list.append(w)
    cost_list.append(cost_val)
    print('第',epoch,'世代',' w = ',w,' loss = ',cost_val)
    
print('训练后预测：',4,forward(4))

输出

训练前预测： 4 0.4
第 0 世代  w =  0.2773333333333333  loss =  16.846666666666668
第 1 世代  w =  0.4381155555555556  loss =  13.84870874074074
第 2 世代  w =  0.583891437037037  loss =  11.384254083055142
第 3 世代  w =  0.7160615695802469  loss =  9.358362823119462
第 4 世代  w =  0.8358958230860906  loss =  7.692990167840783
第 5 世代  w =  0.9445455462647221  loss =  6.323979828639249
第 6 世代  w =  1.043054628613348  loss =  5.198592484911624
第 7 世代  w =  1.1323695299427687  loss =  4.273474071152241
第 8 世代  w =  1.213348373814777  loss =  3.5129856186680826
第 9 世代  w =  1.2867691922587312  loss =  2.8878303112393273
第 10 世代  w =  1.3533374009812495  loss =  2.3739248638525594
第 11 世代  w =  1.4136925768896662  loss =  1.9514717458585313
第 12 世代  w =  1.4684146030466307  loss =  1.6041965071733062
第 13 世代  w =  1.518029240095612  loss =  1.3187208265189987
第 14 世代  w =  1.5630131776866882  loss =  1.084047129213129
第 15 世代  w =  1.6037986144359306  loss =  0.891134920085601
第 16 世代  w =  1.6407774104219104  loss =  0.7325525103068125
第 17 世代  w =  1.6743048521158654  loss =  0.602190721361547
第 18 世代  w =  1.7047030659183846  loss =  0.4950275369912518
第 19 世代  w =  1.7322641130993355  loss =  0.4069346366306757
第 20 世代  w =  1.7572527958767308  loss =  0.3345183572942651
第 21 世代  w =  1.7799092015949025  loss =  0.27498895717843275
第 22 世代  w =  1.8004510094460449  loss =  0.2260531445321019
...
...
训练后预测： 4 7.999577741380291

绘制损失函数

# 绘图
plt.plot(w_list, cost_list)
plt.ylabel('cost')
plt.xlabel('W')
plt.xlim(0,2)
plt.show()

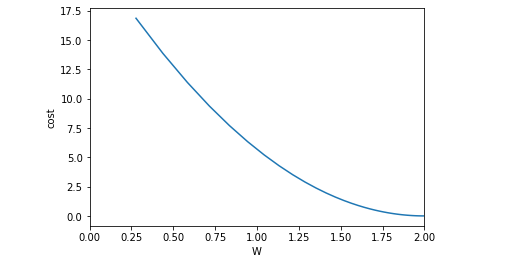
上述损失函数的收敛趋势看起来非常平滑，当实际中可能很少出现这么平滑的损失函数，对于这个问题可以采用指数加权均值的方法来让函数平滑化：
假设 $Ci$ 表示第 $i$ 轮训练的损失值则平滑处理后损失为 $C{i}^{‘}$，则有：

$$C_{i}^{'} = \begin{cases} C_0, & \text {if $i=0$} \\ \beta C_{i}^{'} + (1- \beta)C_{i-1}^{'}, & \text{if $i>0$} \end{cases}$$

这样可以让我们更好地观察收敛的情况！