SegmentTree

线段树

---

 线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。线段树可以在 $O(\log_{2}{N})$ 的时间复杂度内实现单点修改、区间修改、区间查询等操作。

线段树的基本结构

---

为数组（假设下标从1开始）：

$$a[5] = [{1,2,3,4,5}]$$

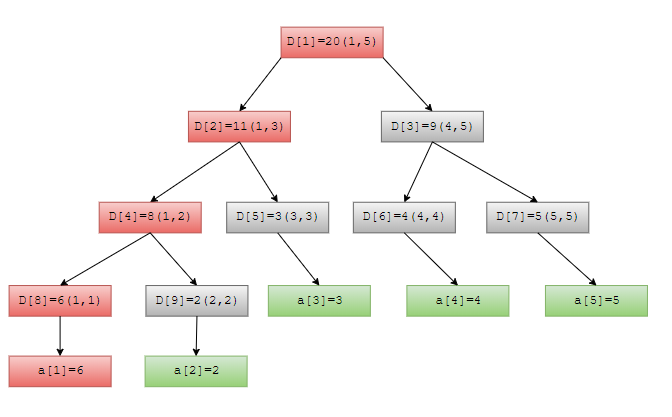
构造线段树如下图（采用堆式存储）：

上述数组 $D$ 用来保存线段树，由于采用的是堆式存储，因此$D[i]$ 的左右孩子结点分别为$D[2\times i],D[2 \times i + 1]$。不难发现上图有两种结点，银色结点括号表示该结点包含的数组 $a$ 的区间，$D[i]$ 的值表示 $\sum_{k=i}^{j}a[k]$。且若区间两端点相等为$[k,k]$则$D[i] = a[k]$即值为绿色结点。

## 线段树的建立

由于树树递归定义的，因此其建立也是递归的：

void buildST(int left, int right, int p, vector<int>& D, vector<int> & a)
{
    if(left == right)
    {
        D[p] = a[left];
        return;
    }
    int mid = left + (right - left)/2;
    build(left, mid, p*2, D, a);
    build(mid+1, right, p*2+1, D, a);
    D[p] = D[p * 2] + D[p * 2 + 1];
}

---

线段树的区间查询

---

区间和：

// [left,right]为待查区间，[cl,cr]为当前区间，p 为当前节点编号，D 为线段树的存储数组
int getSum(int left, int right, int cl, int cr, int p, vector<int> &D)
{
	if(left <= cl && cr <= right) // 当前区间为待查区间的子集
		return D[p];
        // 划分区间，递归查询
	int mid = cl + (cr - cl)/2, sum = 0;
	if(left <= mid) // 与左区间有交集
		sum += getSum(left, right, cl, mid, p * 2, D);
	if(right > mid) // 与右区间有交集
		sum += getSum(left, right, mid+1, cr, p * 2 + 1, D);
	return sum;
}

区间修改：

---

$[cl,cr]$为当前区间，index为要修改的数组$a$的下标，$val$为修改的最终值，$p$为当前节点编号。

void updateST(int cl, int cr, int index, int val, int p, vector<int>& D,vector<int>& a)
{
	if(cl == cr)
	{
		a[index] = val;
		D[p] = val;
		return;
	}
	else
	{
		int mid = cl + (cr - cl)/2;
		if(index >= cl && index <= mid)
			updateST(cl, mid, index, val, p * 2, D, a);
		else if(index > mid && index <= cr)
			updateST(mid + 1, cr, index, val, p * 2 + 1, D, a);
		D[p] = D[p * 2] + D[p * 2 + 1];
	}
}

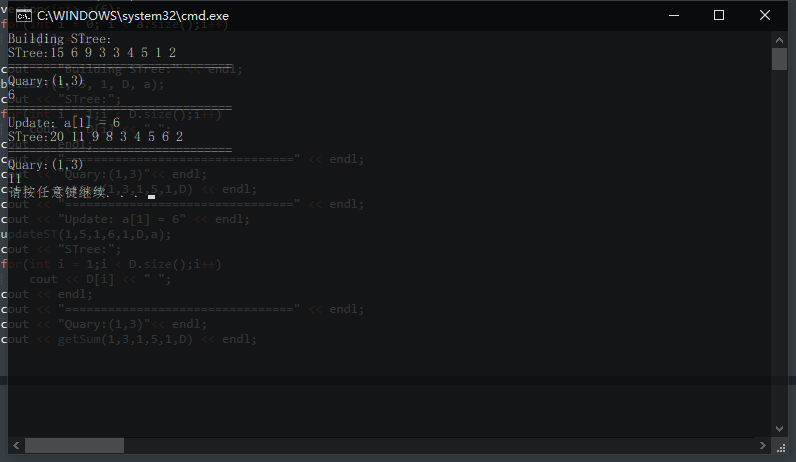
此时如果将$a[1]$ 改成 $6$ ,则树变成(红色表示有修改的节点)：

---

实验

---

int main()
{
	vector<int> D(10,0);
	vector<int> a(6);
	for(int i = 0; i < a.size();i++)
		a[i] = i;

	cout << "Building STree:" << endl;
	buildST(1, 5, 1, D, a);
	cout << "STree:";
	for(int i = 1;i < D.size();i++)
		cout << D[i] << " ";
	cout << endl;
	cout << "================================" << endl;
	cout << "Quary:(1,3)"<< endl;
	cout << getSum(1,3,1,5,1,D) << endl;
	cout << "================================" << endl;
	cout << "Update: a[1] = 6" << endl;
	updateST(1,5,1,6,1,D,a);
	cout << "STree:";
	for(int i = 1;i < D.size();i++)
		cout << D[i] << " ";
	cout << endl;
	cout << "================================" << endl;
	cout << "Quary:(1,3)"<< endl;
	cout << getSum(1,3,1,5,1,D) << endl;

}

结果

---