LeetCode23 合并 K 个排序链表(Hard)

题目描述：

 合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:
[
  1->4->5,
  1->3->4,
  2->6
]
输出: 1->1->2->3->4->4->5->6

题解：

 因为所给链表均有序且头节点指针均在一个数组中，可以将当前数组中的头节点指针所指向的链表节点的值与其所在下标绑定为一个 pair 并存入一个最小堆中（按节点val排序，由优先级队列实现），这样就可以每次从堆中（pop）取出最小值用尾插法插入结果链表中。并且每次pop后都更新lists数组，将新的头节点的 pair 推入最小堆中，如此循环往复直至堆为空。

### 算法演示：  I. 初始化堆：

priority_queue<pair<int,int>,vector<pair<int,int>>> Q;
	//初始化优先级队列，将lists中的元素下标与其所指链表节点的val绑定为pair入堆
	for(int i=0;i<lists.size();i++)
	{
		if(lists[i] != NULL)
		{
                      //加负号取反，间接实现小顶堆
                      Q.push(make_pair(-lists[i]->val,i));
		}
	}

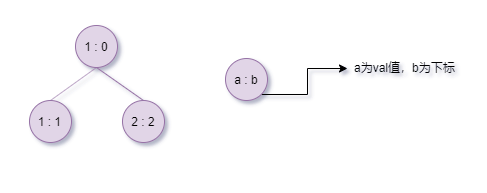
II. 从堆中取出最小元素（堆顶）并更新lists数组与堆

 //实现摘下链表头节点的操作(跟新lists)
	p -> next = new ListNode(-Q.top().first);
	p = p -> next;
	int i = Q.top().second;
	ListNode *r = lists[Q.top().second];
	lists[Q.top().second] = lists[Q.top().second] -> next;
	delete(r);//释放内存
 //弹出顶点
	Q.pop();
//新头节点进入
	if(lists[i]!=NULL)
		Q.push(make_pair(-lists[i]->val, i));

1. 更新lists数组
   
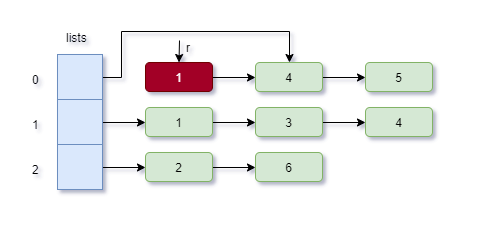
2. 弹出堆顶
   
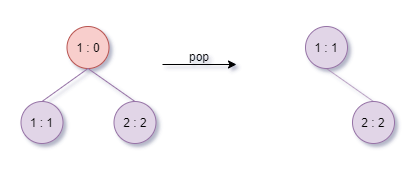
3. 更新堆
   

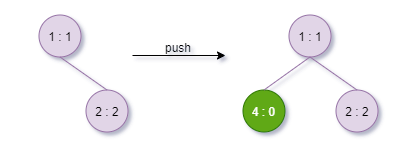
III. 循环II（1、2、3）直到堆为空。

---

算法代码：

ListNode* mergeKLists(vector<ListNode*>& lists)
{
	//定义优先级队列，对pair默认对第一个元素按从小到大排序（大顶堆）
	//因此push进队列时可将对应链表节点的val值取相反数，输出时还原，间接实现了小顶堆
	priority_queue<pair<int,int>,vector<pair<int,int>>> Q;
	//初始化优先级队列，将lists中的元素下标与
	for(int i=0;i<lists.size();i++)
	{
		if(lists[i] != NULL)
		{
			Q.push(make_pair(-lists[i]->val,i));
		}
	}

	//定义结果链表头节点
	ListNode *head = new ListNode(-1),*p = head;
	while(!Q.empty())
	{
		//实现摘下链表头节点的操作
		p -> next = new ListNode(-Q.top().first);
		p = p -> next;
		int i = Q.top().second;
		ListNode *r = lists[Q.top().second];
		lists[Q.top().second] = lists[Q.top().second] -> next;
		delete(r);
		Q.pop();
		if(lists[i]!=NULL)
			Q.push(make_pair(-lists[i]->val, i));
	}
	return head -> next;
}

测试：

//生成链表数组
void generatList(vector<ListNode*>& lists,vector<vector<int>>& list)
{
	if(list.size()!=lists.size()) return;
	for(int i = 0; i < lists.size();i++)
	{
		ListNode* p = lists[i];
		for(int j = 0; j < list[i].size();j++)
		{
			if(p == NULL) { lists[i] = new ListNode(list[i][j]); p = lists[i];}
			else
			{
				p -> next = new ListNode(list[i][j]);
				p = p -> next;
			}
		}
		p -> next = NULL;
	}
}
int main()
{
	vector<ListNode*> lists(3);
	vector<vector<int>> list = {{1,4,5},{1,3,4},{2,6,9}};
	generatList(lists,list);
	ListNode* head = mergeKLists(lists);
	ListNode *p = head;
	while(p)
	{
		cout << p -> val << endl;
		p = p -> next;
	}
	return 0;
}

运行结果：

---

复杂度分析：

 假设 K 个链表每个链表的长度为 N ，堆的调整时间复杂度为 $ \log{2}{K} $，故时间复杂度为$ KN \log{2}{K} $.
 空间复杂度为$ O(1) $.

---

END