最近看了Adam Geitgey的机器学习系列文章。寻思着闲着也是闲着,干脆翻译以下,顺便学习下英语啥的哈哈哈。第一次做这种事,有不到位的地方欢迎指教噢。
前言
你是否已经厌倦了在查阅了无数有关深度学习的文章之后仍然不能参透其中深意的无力感。如果有的话,现在,是时候改变现状了!
现在,我们将学习如何应用深度学习知识编写一个程序去识别图像中的物体。换句话说,我们将试着去清楚地解释谷歌相册具有的黑科技图像搜索功能(根据图像内容搜索图像)内部究竟如何运作,揭开其神秘的面纱。
就像Part1和Part2那样,这篇教程是面向所有对机器学习有着极度的好奇但却不知道该从何处开始的同学。写作本教程的目的旨在它能够对所有人而言都是通俗易懂的,因此我使用了大量的概括斌且略过了大量的非必要的细节。但这些并不重要,我才不会在意这些。只要能让读者加深对学习机器学习兴趣(而不是畏惧),我的任务就算圆满完成了。
(如果你还没读过Part1和Part2,那么现在就可以去读读啦!)
利用深度学习识别对象

你以前也许看过上面这副著名的xkcd 系列漫画。
该暗讽基于这样的一个事实:随便一个三岁小孩都能认出一张图片中的鸟,但搞清楚如何让计算机识别物体这个问题却令世界上最好的计算机科学家困惑了50余年。
但近些年来,我们终于摸索出一套利用 深度卷积神经网络 识别物体的方法。这个词听起来就像是从威廉·吉布森的科幻小说中摘抄下来的一样,但是如果你将其逐一分解开来,这个方法是很好理解的。
那么,让我们开始吧—编写一个能够识别鸟类的程序!
一个简单的开始
在学习如何识别图像中的小鸟之前,先让我们来学习一下更为简单的识别任务—识别手写数字 ” 8 “。
在本系列的第二部分,我们学习了通过将大量简单的人工神经元链接在一起所组成的神经网络可以解决一些复杂的问题。我们创建了一个小型的神经网络根据房子的大小、房间数目以及其所在的社区去估计该房子的市场价格:
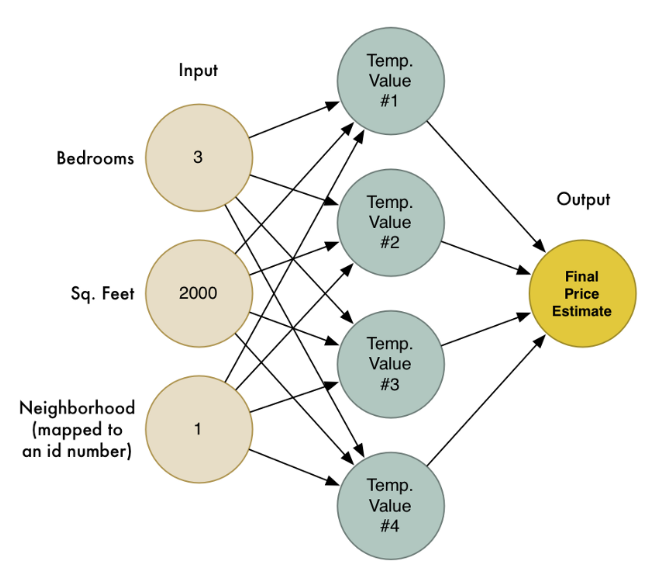
我们也认识到机器学习的目的就是用一个通用算法可以被喂以不同的数据以解决不同的问题。因此让我们修改之前写过的神经网络让它具有识别手写数字的能力。但为了使这项工作更加简单,我们只尝试去识别一个数字 ——- 8 。
让机器学习算法正常工作的前提是你必须拥有数据——最好是非常多的数据。所以我们需要大量的手写数字8的图片好让我们可以开始工作。幸运的是,研究者们早已为此创建了一个叫做MNIST的手写数字数据集。MNIST数据集提供了60,000张$18\times 18$像素的手写数字图片。
这里有些来自MNIST的关于手写数字8的图片:

如果你细想一下,一切都只是数字而已
我们在第二部分所构建的神经网络仅仅只有三个输入结点(”3“个房间、”2000“平方英尺等等)。但现在我们想让我们的神经网络处理图像,我们如何将图像输入网络而不仅仅是数字?
问题的答案简单到让人难以置信。一个神经网络以数字作为其输入。对于计算机而言,一张图片实际上只是一个数字网格,网格中的每个数字表示对应像素的明暗程度:
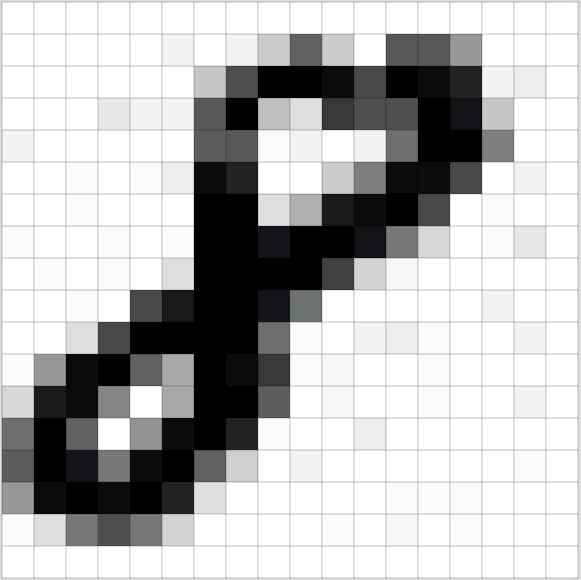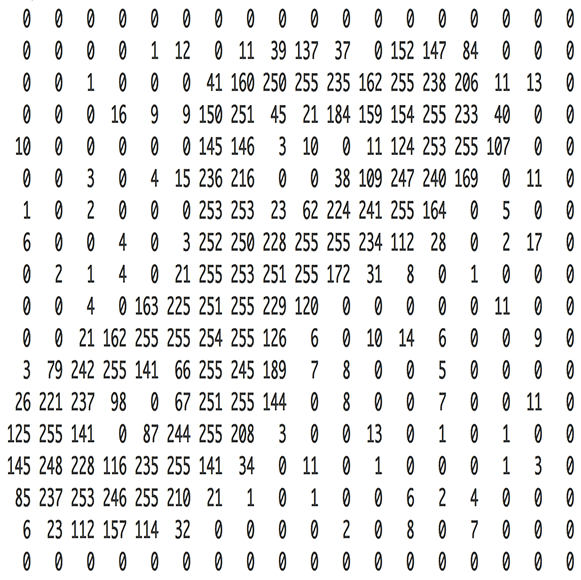
为了将一张图片输入我们的神经网络,我们简单地将一张$18\times 18$像素的图片视为一个含有$18\times 18=324$个数字的数组:

为了处理这324个输入,我们只要扩大输入层结点至324个就可以了。
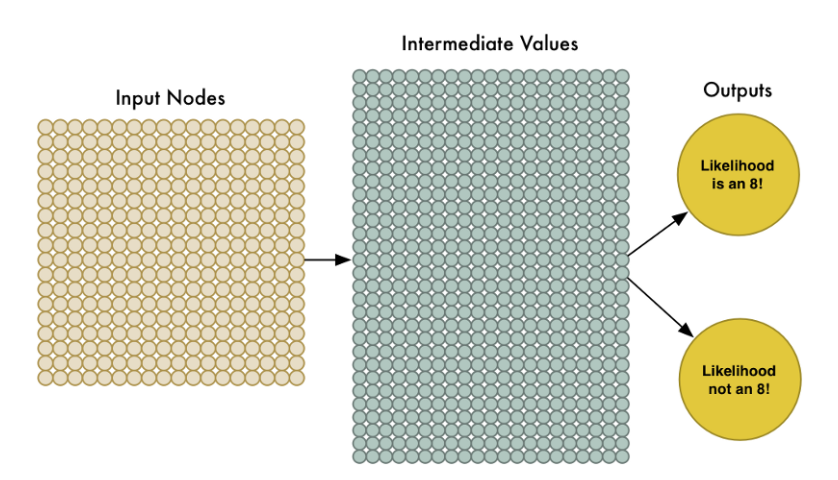
注意到我们的神经网络现在也只有两个输出结点(之前是一个)。第一个输出表示该图片是8的概率,第二个表示该图片不是8的概率。通过为我们想要识别的每种类型的对象提供单独的输出,我们可以利用神经网络对对象进行分类。
现在我们的神经网络的确比之前的规模大得多了(用324个输入结点代替了3个输入结点)。但是大多数现代计算机都能够在眨眼间处理完拥有数百神经元结点的神经网络。甚至你的手机也可以做到这般。
剩下的就是用这些 ” 8 “ 的图片以及不是 ” 8 “ 的图片来训练神经网络使其能够区分二者了。我们会人为地告知网络那些真正的” 8 “ 的图片是8的可能性为100%,而其他图片是8的可能性为0%。
下面是部分训练集的数据:

对于如此规模类型的神经网络,我们只需在一台现代笔记本电脑上花费几分钟时间就可以训练出一个能够识别手写数字8的高准确度的神经网络模型。
欢迎来到(20世纪80年代后期)图像识别的世界!!!
以管窥天
简单地将一个个像素馈入神经网络,这很简洁,也的确可以用来构建图像识别神经网络。机器学习太牛皮了!…但这样真的就完美了吗?
吼,当然没有那么简单了。
首先,好消息是我们的【数字8识别者】在识别居中字符时的确可以很好地工作并且拥有很高的准确率:

但坏消息是:
【数字8识别者】对于非居中字符的识别效率惨不忍睹,仅仅一丢丢的位置变化就毁了它的一世英名:

这是因为我们的神经网络仅仅学习了具有完美的居中位置的数字8图像,所以它仅仅只能够区别位于居中位置的数字图像。
这种能力在现实世界中毫无用处。现实世界的问题往往不那么简单明了。所以,我们必须搞清楚如何使我们的神经网络对于非居中字符图像也能准确识别。
蛮力解法 #1:使用滑动窗口搜索
我们以及构建了一个表现不错的识别居中字符8的神经网络。那如果我们仅仅只是扫描非居中的8的图像直到找到它为止。这样我们就可以利用先前的神经网络来识别它了不是吗?就像下图这样:
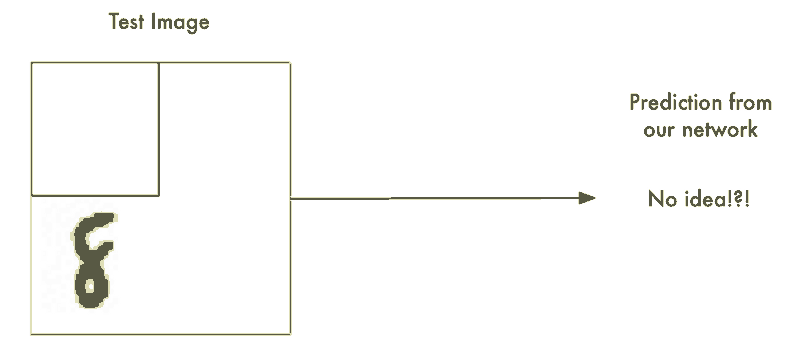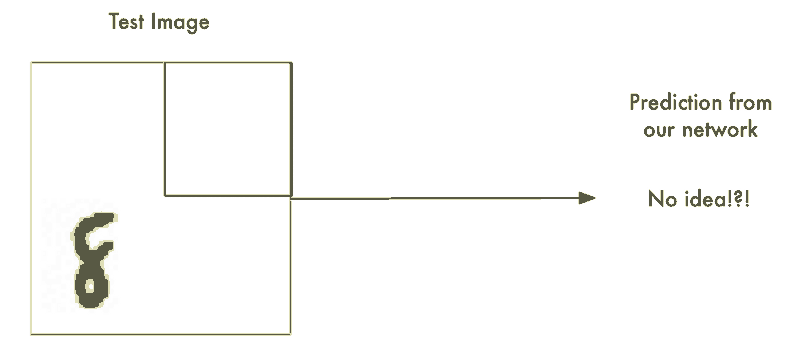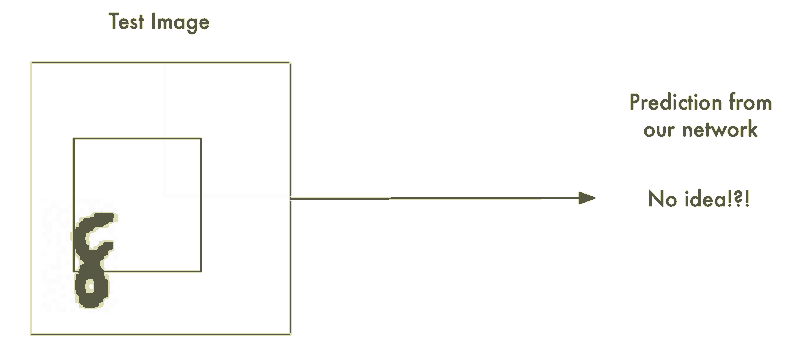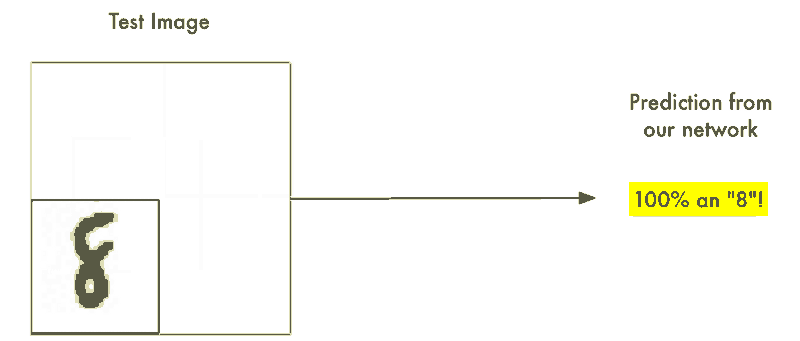
这种方法叫做滑动窗口法。它是一个依靠蛮力的解决办法(可不怎么聪明)。它在有限的案例中表现还算不赖,但它实在是太低效了。你不得不一遍又一遍地检查相同的图像寻找不同大小的数字图像。我们应该能够做的更好,而不是得过且过。
蛮力解法 #2:更多数据以及更深层的网络
当我们训练神经网络时,我们仅仅向其投喂数字8居中的图像。如果我们向他投喂更多的数据,包括数字8不居中以及不同大小的图像又会怎样呢?
我们甚至不需要去收集新的训练数据,只需要写一个脚本让其自动生成位于图片不同位置不同大小的8的图像即可:

利用这项技术,哦我们可以轻松地创建无数的数据用于训练。
更多的数据对于我们较小的神经网络意味着困难重重。但我们可以扩大它的规模,以至于让它能够学习更复杂的模式。
为了扩大神经网络的规模,我们可以增加其隐藏层(及其结点)的数量:
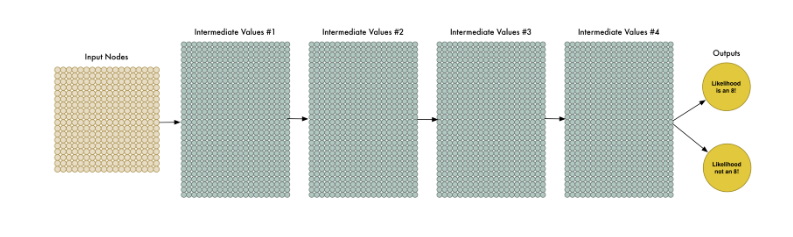
我们将这个新面孔称为” 深度神经网络 “,因为它对比传统神经网络有着更多的层数。
自20世纪60年代后期以来,这个想法就被提出了。但是直到近些年,训练这么大的神经网络还是太慢了以至于让它看起来毫无用处。但是一旦我们搞清楚如何用3D 图形卡(被设计成用来快速进行矩阵乘法)来代替普通的计算机处理器,使用大型神经网络就会变得切实可行了。事实上,你用来玩OverWatch的NVIDA GeForce GTX 1080显卡就完全可以用来快速训练神经网络。

但是即使我们可以构建自己的大型神经网络并且用3D 显卡来训练它,这仍然不会让我们能够高枕无忧。对于如何处理图像并将其传入神经网络中,我们需要更加聪明一点。
仔细想想。分别训练神经网络去识别图像顶部的8以及图像底部的8是毫无意义的,因为它们根本就是两八竿子打不着边的独立对象。
肯定有一些方法能够使得神经网络具有足够的智能,能够知道图像中任何位置的8都是相同的,而不需要任何额外的训练。幸运的是,还真有!
终极解决方法就是:卷积
作为一个人类,你直观地知道图片具有层次结构或者概念结构。琢磨一下下面这张图片:

生而为人,你可以立刻识别出这张图片的层次结构:
- 这块地被混凝土以及草坪所覆盖
- 图中有个小男孩
- 小男孩坐在一只玩具马上面
- 玩具马在草坪上面
重点在于,无论这个孩子站在那种地表上(混凝土、草坪、瓷砖等等)我们都会意识到他的存在,也就是我们不用去学习各种孩子站在不同地表上的图像。
但是现在,我们的神经网络无法做到这些。它认为相同的”8“(孩子)位于图像的不同位置(地表)是完全不同的情况。它无法明白在图片上移动一个对象并没有改变该对象的本质。这就意味这它必须再学习各种对象处于不同位置的图像。这真是逊👎爆了。
我们需要让我们的神经网络理解平移不变性——无论它出现再图片任何地方,8 就是 8。
我们将用卷积来完成这项工作。这个方法的灵感来源于计算机科学与生物学(疯狂的科学家们用奇怪的探针来拨开猫脑以期弄清猫脑是如何处理图像的)。
卷积的工作原理
并非将整个图像网格的数字都喂入我们的神经网络,而是利用一些更加聪明的方法:无论一个对象位于图片的哪个位置,它还是它,并无二意。
下面一步一步地介绍了卷积的工作过程。
Step1: 将图像分解为图像切片
类似于我们用滑动的窗口在图片上扫描一样,让窗口在整个原始图像上扫描,并记录存储每次扫描到的小块区域图像。

通过这项工作,我们将上述图像分成了77块相同尺寸的小图切片。
Step2: 将每张图像切片馈送到一个小的神经网络中
早些时候,我们将单个图片馈入一个神经网络并观察它的对数字8的输出判断。现在我们在做同样的事情,只不过现在我们输入的是一个个小的图像切片,而不是一整个图片:
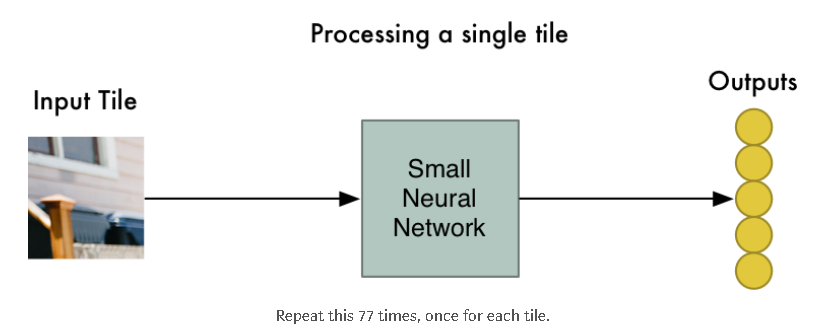
然而,这儿有一个大的区别是:我们将为同一原图片的每一个小的图像切片保留相同的神经网络权值。换句话说,我们将平等地对待每一张图像切片。如果在某一切片上有些特别的事情发生,我们将会标记它。
Step3: 将每一个切片的结果保存到一个新的阵列中
我们不想失去各个切片的的原有顺序,所以我们将处理后的结果按顺序保存到一个与原始图像布局相同的网格中。就像这样:

换句话说,我们从一张大图片开始,最后我们用一个稍微小一点的阵列来记录我们原始图像的哪些部分是异常的。
Step4: 下采样
步骤3的结果是一个阵列,用来确定(maps out映射出来)原图的哪些位置是异常的。但是这个数组还是太大了:

为了减少该阵列的尺寸,我们应用 最大池化算法(Max Pooling) 对它进行下采样。这听起来像是痴人说梦,但事实并非如此!
我们将目光放在每一个$2\times 2$网格上并仅保留其中(4个数)的最大值:
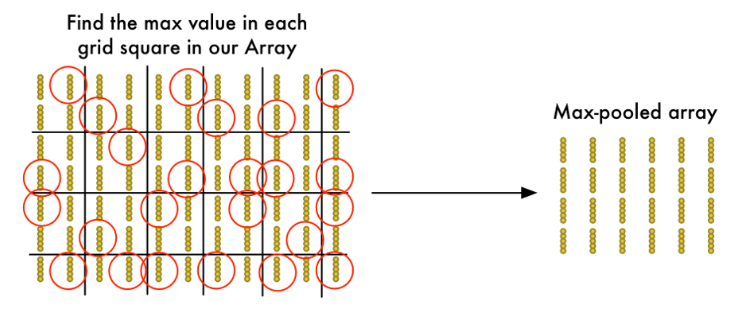
关键在于如果我们在构成每个$2\times 2$网格方块的四个输入图块中的任何一个中发现了一异常的东西,我们将保留最值得关注的那个。这样就可以减少阵列的大小,同时保留追重要的部分。
Final step: 做一个预测
到目前为止,我们已经将原始的巨大的图像阵列变成了一个相当小的阵列了。
你猜怎么着?现在的阵列仅仅是一小堆数字而已,因此我们可以以它作为输入投喂到另一个神经网络中了。这个最终的神经网络将会决定该输入原始图像是否匹配。为了区别于卷积步骤,我们称它为” 全连接网络 “。
所以从头到尾,我们的整个五步走战略看起来像这样:
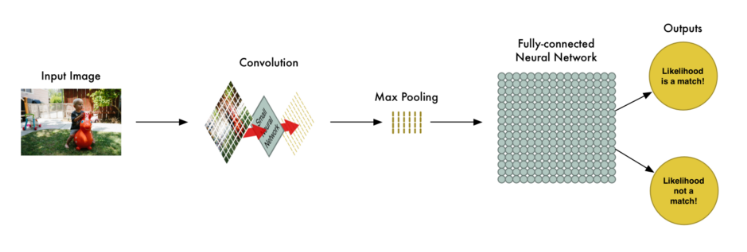
添油加醋
让我们在脑海中想象一下整个的一系列步骤:卷积、最大值池化、输入全连接网络。
在现实世界中解决一个问题时,这些步骤可以被结合甚至可以根据需要堆叠多次!两个、三个、甚至10个卷积层都可以。你还可以应用最大值池化操作来缩小你的数据规模。
最根本的想法时从一个大图像开始,一步一步地将其浓缩提取,知道你最终得到一个想要的结果。你的卷积操作越多,你的神经网络就会学习到更多的图像特性。
举个栗子,第一次卷积操作可能让神经网络学习到了识别图像尖锐的边缘,第二次卷积操作就可能利用先前学到的有关尖锐边缘的知识去识别鸟的喙了,而第三次卷积则可能利用喙的知识来识别出整个鸟了,等等。
下面是一个更符合实际的深度卷积神经网络(就像你会在研究论文中看到的一样)的样子:
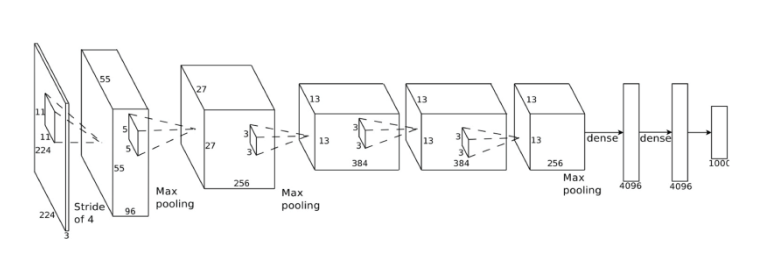
在上图的例子的神经网络中,它接受一个$224\times 224$像素大小的图像,其两次应用卷积和最大值池化,三次引用卷积操作并且拥有两层全连接层。最终的输出结果是对应1000中类别的概率。
构建正确的网络
那么,你如何知道入药合并哪些步骤才能使你的神经网络(分类器)正常工作呢?
老实说,想要正确地回答这个问题你不得不去做大量的试验和测试。在你遭到最佳的结构和参数去解决你的问题前,你也许不得不去训练100个神经网络。机器学习需要大量的反复试验。
构建我们的鸟类分类器
现在我们终于有足够的知识去编写一个可以识别鸟类(是鸟/不是鸟)的程序了。
一如既往地,我们需要一些数据。免费的CIFAR10 数据集包含了6,000张鸟类的图片和52,000张非鸟类图片。但是为了得到更多的数据我们也将加入Caltech-UCSD Birds-2002001 数据集,它包含了12,000张鸟类的图片。
下面是一些我们将采用的数据集中的部分图像:

还有52,000张非鸟类图像中的一些:

这些数据集可以很好地应用在我们的目的上。但是72,000低分辨率的图像对于真实世界的应用来说仍然很小。如果你想让你的神经网络达到Google的级别的性能的话,你需要数以百万计的大图像。在机器学习领域,数据量的重要性几乎盖过了一个好的算法。现在你知道为什么Google热衷于为你提供图像存储服务了吧,他们要的是你的数据!
为了构建我们的鸟类分类器,我们将使用python的TFLearn库,TFLearn是Google的Tensorflow深度学习库的包装器,它公开了一个简化了的API。这使得构建卷积神经网络变得像写几行代码来构建网络层一样简单。
下面的代码定义并训练了一个神经网络:
1 | # -*- coding: utf-8 -*- |
如果你使用快拥有足够显存的显卡(比如Nividia GeForce GTX 980 或更好的),会在一个小时之内训练完成。如果你用的是普通的CPU的话,可能会耗费很长时间。
随着训练的进行,模型的准确性会逐渐提高。第一轮训练过去后,我得到了75.4%的准确率。十轮过去后,已经有91.7%了。而在50轮后,达到了95.5的准确率。之后传统的训练再无提升,我便停止了训练。
&emps;恭喜恭喜!我们的程序已经可以识别鸟类图像啦!
测试我们的网络
现如今我们有了一个传统的神经网络,我们可以利用它这里有个简单的脚本可以向网络输入一个图片并预测改图中是否有鸟类。
但是为了了解我们的神经网络的效能究竟如何,我们需要用更多的图片来测试它。我所创建的数据集保留了15,000图片以供验证。当我用15,000张图像测试神经网络时,他的预测准确率达到了95%。
这个结果看起来很不错,事实真的如此吗?这得看情况!
%95的准确率究竟如何?
我们的神经网络声称具有95%的准确率。但是魔鬼常常隐藏在细节之中。这可能意味着各种各样的事故。
举个栗子,如果我们的训练数据集中仅有5%的图片是鸟类而95%的图像是其他东西呢?当然,每次识别是不是鸟的准确率高达95%,但它明显毫无用处(一个程序即使每次都猜不是鸟,他的准确率也能达到95%)。
相较于整体准确率,我们必须更多地关注数字本身。为了更好地判断分类系统的真正性能,我们必须更多地关注它的具体的错误情况,而不仅仅是他的错误率。
让我们将神经网络的输出结果分成多种类别,而不是只是判断对错这两种情况:
- 首先,这里有一些我们的神经网络能够正确地将其识别为鸟类的图片。姑且称它们为 真正类:

- 其次,这里有一些我们的神经网络能够准确地将其识别为非鸟类的图片。姑且称它们为 真负类:

- 再者,这里有一些被识别为是鸟但事实上不是鸟的图片(诸如飞机等),这些是我们的 假正类:

- 最后,这里有一些鸟类的图片,但却无法正确识别它们为鸟类。这些是我们的所谓 假负类:

利用我们的拥有15,000张图片的验证集,下面列出了我们的预测落入每一个类别的次数:
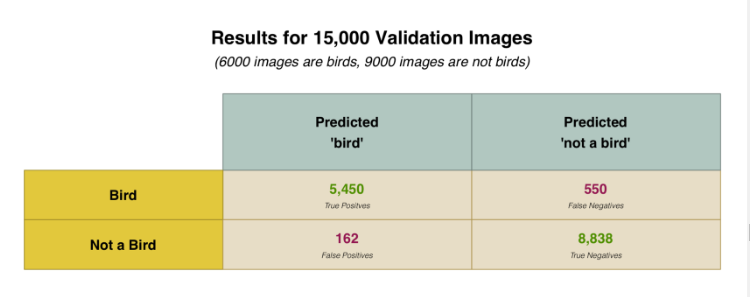
为何我们要将结果拆分成这样?因为并非所有的错误都是相同的。
现象一下如果想要编写一个程序从核磁共振图像中检测肿瘤。如果我们检测到癌症,我们宁愿它是假阳性而不是假阴性。假阴性或许是最糟糕的情况了(当程序告诉一个为患癌症的人他没有癌症时)。
我们不仅仅考虑整体准确率,并且计算精度和召回指标。精度和召回的指标让我们更清楚地了解神经网络的具体表现:

我们的决定无比正确!上述结果告诉我们识别鸟类的准确率高达97%。但也告诉我们我们只正确识别了数据集中的的90.83%的鸟类图片。换句话说,我们也许并没有找到数据集中所有的鸟类图片,但当我们找到它时,我们的预测答案具有很高的准确度。
扬帆起航
现在你已经对基本的深度神经网络有了了解,你可以尝试使用tflearn附带的一些示例,以便用不同的神经网络架构来解决问题。它甚至还带有内置的数据集,因此你甚至无需去寻找数据集。
你也有足够的知识去学习机器学习的其它内容了。试试如何用算法去训练计算机自己打雅达利游戏如何?
作者:Adam Geitgey
英文原文链接:Machine Learning is Fun! Part 3: Deep Learning and Convolutional Neural Networks
