作为本系列的第一篇文章,本文仅对卷积神经网络的工作过程做一个简单的介绍,并不涉及数学原理与推导。若想要深入了解数学原理,那么可以去查看相关文献或者我将会在之后更新相关内容的文章。
阅读这篇文章前你最好对简单的神经网络有一定的了解,如果没有,可以参看博主的神经人工神经网络学习笔记系列文章。
如果你已经做好了准备,那就让我们开始吧!
什么是卷积神经网络?
卷积神经网络(Convolutional Neural Network,CNN)是前馈人工神经网络的一种。在图像识别领域有着广泛的应用并且非常有效。当人们谈到计算机视觉时,通常都绕不开卷积神经网络。
计算机眼中的图像
毫无疑问,你可以很快分辨下图中的动物是只猫。但在计算机“眼中”,它仅仅是一个数字序列。图像由一个个像素组成,每一个像素通常以RGB(Red,Green,Blue)三原色表示。但为了简化,我们使用灰度(0-255)表示,仅仅一个数字就可以表示(0:黑色 255:白色)。如此一来,对于一张$200\times 200$像素的图片,在计算机眼中就为一个$200\times 200$的矩阵,也即一个$40000$维的向量。

计算机学习(训练)识别图像的过程就是将许多图片向量输入某种算法处理后将结果与目标值相比对,对误差进行修正直到结果输出令人满意为止。待训练结束后再给它看一个从未看过的图像它也能准确地识别图像的内容。
本系列文章我们将继续使用Mnist数据集来训练和测试神经网络。
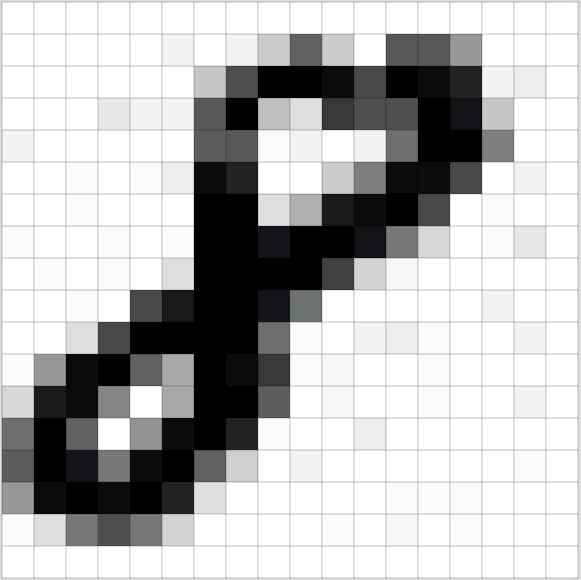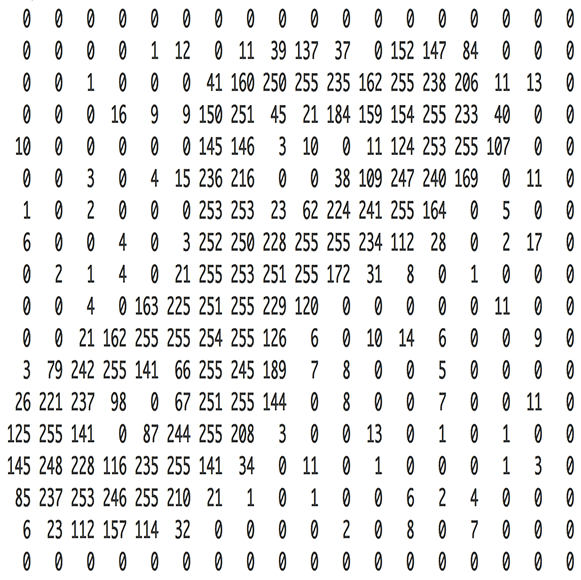
LeNet框架(20世纪90年代)
LeNet框架是卷积神经网络的祖师爷LeCun在1998年提出的,用于解决手写数字识别的视觉任务。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。本篇文章也将围绕该框架来进行卷积神经网络的介绍。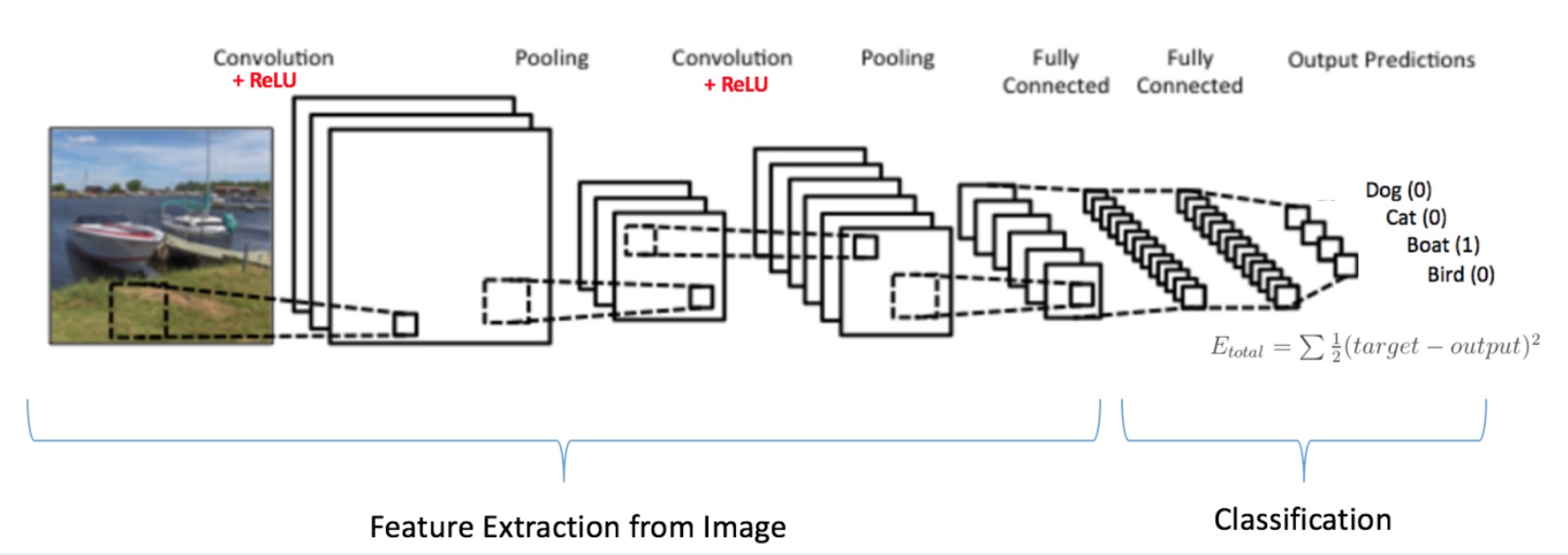
LeNet 卷积神经网络的工作过程
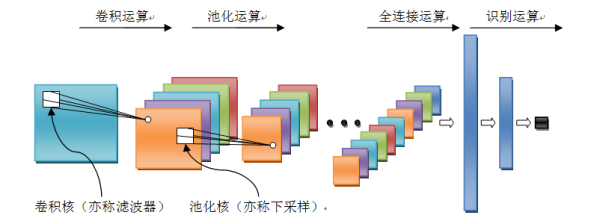
1、卷积运算:
顾名思义,卷积神经网络得名于“卷积”运算。在卷积神经网络中,卷积的主要目的是从目标图像中提取“特征”。通过使用输入数据中的小方块(矩阵分块)来学习图像特征,卷积运算保留了像素间的空间关系。
正如前文所说,每个图像都可以被计算机看成是一个像素值矩阵。现仅考虑一个$5\times 5$像素的图像矩阵$W_{img}$:

再令一个$3\times 3$的矩阵$W_{f}$:

将$3\times 3$的矩阵在$5\times 5$矩阵上移动并将对应位的数值相乘并求和,得到一个新的矩阵即为卷积运算后的特征值矩阵:

这个由特征值组成的矩阵被称为 卷积特征 或 特征映射 。而上述参与卷积运算的$3\times 3$矩阵被称为 卷积滤波器 或 核 或 特征探测器 (以下统称滤波器,但是事实上过滤器的作用就是原始图像的 特征检测器)。上述例子中过滤器在图像矩阵上每次移动1个像素单位,称为 步幅 。
不难发现,不同的滤波器作用于相同图像上会得到不同的特征映射,下图列出了一些滤波器的取值以及功能作用(边缘检测,锐化等):

总的来说,一个滤波器在输入图像上移动(卷积操作)以生成特征映射。在同一张图像上,另一个滤波器的卷积生成了不同的特征图。需要注意到,卷积操作捕获原始图像中的局部依赖关系很重要。还要注意这两个不同的滤波器如何从同一张原始图像得到不同的特征图。请记住,以上图像和两个滤波器只是数值矩阵。
实际上,卷积神经网络在训练过程中会自己学习这些滤波器的值(尽管在训练过程之前我们仍需要指定诸如滤波器数目、大小,网络框架等参数)。我们拥有的滤波器数目越多,提取的图像特征就越多,我们的网络在识别新图像时效果就会越好。
特征映射(卷积特征)的大小由我们在执行卷积步骤之前需要决定的三个参数控制:
- 深度:深度对应于我们用于卷积运算的过滤器数量。在图6所示的网络中,我们使用三个不同的过滤器对初始的船图像进行卷积,从而生成三个不同的特征图。可以将这三个特征地图视为堆叠的二维矩阵,因此,特征映射的“深度”为3。

- 步幅:步幅是我们在输入矩阵上移动一次过滤器矩阵的像素数量。当步幅为1时,我们一次将过滤器移动1个像素。当步幅为2时,过滤器每次移动2个像素。步幅越大,生成的特征映射越小。
- 零填充:有时,将输入矩阵边界用零来填充会很方便,这样我们可以将过滤器应用于输入图像矩阵的边界元素。零填充一个很好的特性是它允许我们控制特征映射的大小。添加零填充也称为宽卷积,而不使用零填充是为窄卷积。
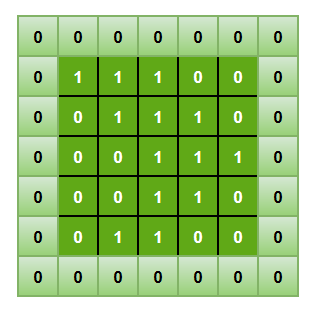
2、非线性操作(ReLU操作)
每次卷积操作之后,都会进行一次ReLU操作,其全称为修正线性单元(Rectified Linear Unit),是一种非线性操作。以下为修正线性函数的图像及表达式:

ReLU 是一个针对元素的操作(应用于每个像素),并将特征映射中的所有负像素值替换为零。ReLU 的目的是在卷积神经网络中引入非线性因素,因为在实际生活中我们想要用神经网络学习的数据大多数都是非线性的(卷积是一个线性运算 —— 按元素进行矩阵乘法和加法,所以我们希望通过引入 ReLU 这样的非线性函数来解决非线性问题)。
从可以很清楚地理解 ReLU 操作。它展示了将 ReLU 作用于某个特征映射得到的结果。这里的输出特征映射也被称为“修正”特征映射。

其他非线性函数如 Sigmoid 或 tanh 也能达到类似效果,但是 ReLU 函数的效果是最好的。
3、池化(Pooling)
空间池化(也称为子采样或下采样)可降低每个特征映射的维度,并保留最重要的信息。空间池化有几种不同的方式:最大值,平均值,求和等。
在最大池化的情况下,我们定义一个空间邻域(例如一个2 × 2窗口),并取修正特征映射在该窗口内最大的元素。当然我们也可以取该窗口内所有元素的平均值(平均池化)或所有元素的总和。在实际运用中,最大池化 的表现更好。
下图展示了通过2 × 2窗口在修正特征映射(卷积+ ReLU 操作后得到)上应用最大池化操作的示例:
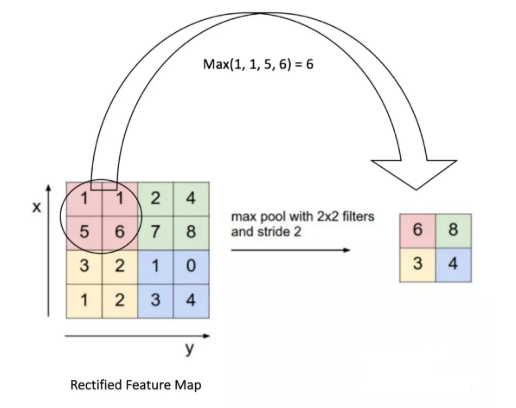
我们将2 x 2窗口移动2个单元格(也称为“步幅”),并取每个区域中的最大值。如图9所示,这样就降低了特征映射的维度,变成了一个$2\times 2$的矩阵。
由于池化操作分别应用于每个特征映射(因此,我们从三个输入映射中得到了三个输出映射)。
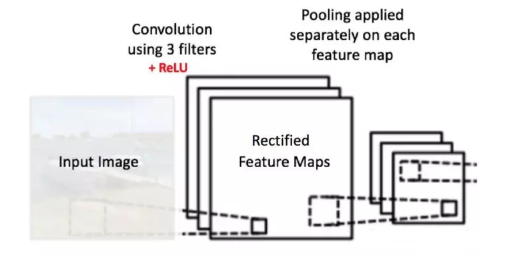
两种池化方法的结果对比:

池化的作用是逐步减少输入的空间大小。具体来说有以下四点:
- 使输入(特征维度)更小,更易于管理
- 减少网络中的参数和运算次数,因此可以控制过拟合
- 使网络对输入图像微小的变换、失真和平移更加稳健(输入图片小幅度的失真不会改池化的输出结果 —— 因为我们取了邻域的最大值/平均值)
- 可以得到尺度几乎不变的图像(确切的术语是“等变”)。这是非常有用的,这样无论图片中的物体位于何处,我们都可以检测到
目前为止,我们已经了解了卷积神经网络中 卷积、ReLU、池化 的工作原理。这一点非常重要,下面我们将举例来描述这一过程。
可视化卷积神经网络
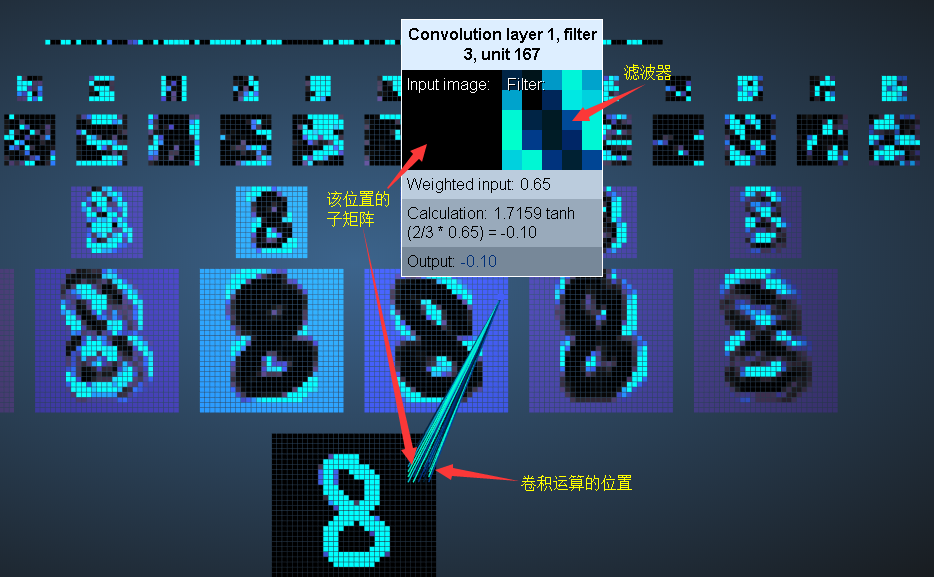
Adam Harley 创建了一个基于 MNIST 手写数字数据集训练卷积神经网络的可视化。我强烈推荐大家 使用它来了解卷积神经网络的工作细节。其链接如下,可以自行尝试:

1、卷积层
将鼠标放在卷积层的某个像素点上并点击会出现:
2、池化层

3、全连接层
全连接层的每一个结点都与其前一层的每一个结点相连接。


该可视化项目还有3D版的,大家可以去玩玩,对于加深理解很有帮助。
