人工神经网络学习笔记（1）

如何让网络可以学习

上一篇文章中的神经网络还没有学习能力，这好比如说该网络只接收外部输入并输出结果，却没有反馈机制没有对结果进行正确性分析，让我们以小明与老师之间的对话来比喻这种情况：

• 老师：1+1=？
• 小明：6
• 老师：1+2=？
• 小明：2
• …

可以发现，当小明给出答案后老师并没有给于他反馈。因此小明可能某一次猜中了正确答案，但只是凑巧而已，他不具备学习能力。
现在让老师给点反馈：

• 老师：1+5=？
• 小明：4
• 老师：少了
• 小明：5
• 老师：少了
• 小明：6
• 老师：正确，你真棒！
  这样子，小明学会了1+5=6.
  
  我们的神经网络也需要具备这样的学习能力。
  也就是说，当网络输出错误的结果时要有一个改变下一次输出的机制。想要改变输出，可以改变哪些量呢？
  观察输出函数： $$O_{output}= \left[ \begin{matrix} Sig(\sum_{j=1}^{3}{w_{j,1}\cdot i_{oj}}) \\\\ Sig(\sum_{j=1}^{3}{w_{j,2}\cdot i_{oj}}) \\\\ Sig(\sum_{j=1}^{3}{w_{j,3}\cdot i_{oj}}) \\\\ \end{matrix} \right]=\left[\begin{matrix}o_1\\\\o_2\\\\o_3\end{matrix}\right]$$ 不难发现，输出值与以下参数有关：

1. SigMoid函数
2. 链接权重
3. 输入值

显然，我们不可能去左右网络的输入值，因为那是网络要求解的问题，不可能以改变问题的方式改变答案。那么改变激活函数sig如何？这太麻烦了，试想那么多的神经元每一个都不同的激活函数会对运算造成大麻烦，将无法采用简洁的矩阵运算。
因此，改变链接权重会是一个好办法。

---

学习能力的养成

我们已经知道可以通过改变链接权重来改变网络的输出值，使其符合预期。那么问题又来了：

1. 改变权重的依据是什么？
2. 如何改变？
3. 改变的幅度多大合适？

---

改变的依据

改变权重的目的是让输出值与期望值越接近越好（误差值越小越好），因此误差就是依据。所谓误差就是期望值与网络输出值的差：

$$E=t-o$$

我们知道输出层的误差为：$E_o=t_n-o_n$，但是其他层结点的误差是不知道的，因为其他层并没有一个输出期望值$t_n$。
不难发现，最终输出层造成的误差是所有层共同作用的结果，所以可以将总误差分摊给其他层。

误差的反向传播

---

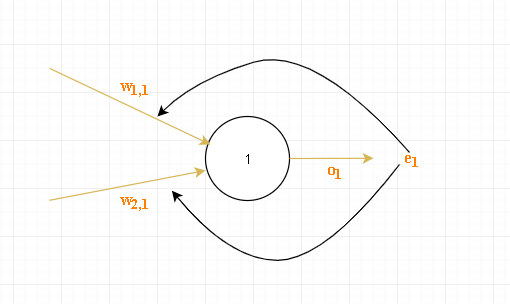
如上图误差为$e_1$，因为链接权重越大说明对该误差的影响越大，因此以链接权重来决定每条链路所分摊误差的大小：

$$e_{w_{1,1}}=\frac{w_{1,1}}{w_{1,1}+w_{2,1}}\cdot e_1$$ $$e_{w_{2,1}}=\frac{w_{2,1}}{w_{1,1}+w_{2,1}}\cdot e_1$$

反向传播误差到更多层中：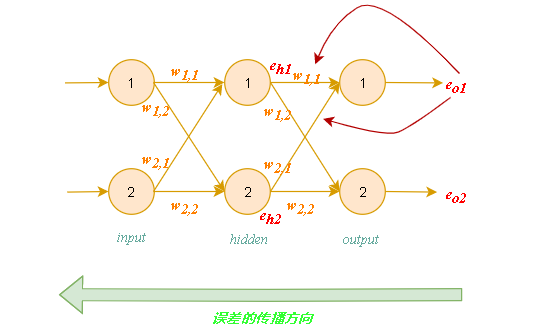

隐藏层结点的误差值：

$$e_{h1}=\frac{w_{1,1}}{w_{1,1}+w_{2,1}}\cdot e_{o1}+\frac{w_{1,2}}{w_{1,2}+w_{2,2}}\cdot e_{o2}$$

---

使用矩阵乘法简化误差反向传播

1. 误差向量： $$error_{output}= \left( \begin{matrix} e_1 \\\\ e_2 \end{matrix} \right)$$
2. 隐藏层误差： $$error_{hidden}= \left( \begin{matrix} \frac{w_{1,1}}{w_{1,1}+w_{2,1}} & \frac{w_{1,2}}{w_{1,2}+w_{2,2}} \\\\ \\\\ \frac{w_{2,1}}{w_{1,1}+w_{2,1}} & \frac{w_{2,2}}{w_{1,2}+w_{2,2}} \end{matrix} \right) \cdot \left(\begin{matrix}e_1 \\\\ e_2 \end{matrix} \right)=\left(\begin{matrix}e_{h1}\\\\e_{h2}\end{matrix}\right)$$ 上述矩阵乘法太过复杂，无法通过简单的矩阵运算求解。观察上式可知，最重要的事情是输出误差链接权重$w_{j,k}$的乘法。较大的权重携带较大的误差给隐藏层，这些分数的分母是一种归一化因子。如果我们忽略掉这个因子，我们仅仅只是失去了后馈误差的真实值大小，但并没有失去其表示的真正含义（影响力）,也就是说反馈误差始终是以链接权重的强度来分配的。因此上式可以简化为： $$error_{hidden}= \left( \begin{matrix} w_{1,1} & w_{1,2} \\\\ w_{2,1} & w_{2,2} \end{matrix} \right)\cdot \left(\begin{matrix}e_1\\\\ e_2\end{matrix}\right)=\left(\begin{matrix}e_{h1}\\\\e_{h2}\end{matrix}\right)$$ 不难发现，隐藏层至输出层的链接权重矩阵$W_{hidden\rightarrow output}$为: $$W_{hidden\rightarrow output}= \left( \begin{matrix} w_{1,1} & w_{2,1} \\\\ w_{1,2} & w_{2,2} \end{matrix} \right)=\left( \begin{matrix} w_{1,1} & w_{1,2} \\\\ w_{2,1} & w_{2,2} \end{matrix} \right)^T$$ 因此： $$error_{hidden}=W_{hidden\rightarrow output}^T\cdot error_{output}= \left( \begin{matrix} w_{1,1} & w_{2,1} \\\\ w_{1,2} & w_{2,2} \end{matrix} \right)^T\cdot \left(\begin{matrix}e_1\\\\ e_2\end{matrix}\right)=\left(\begin{matrix}e_{h1}\\\\e_{h2}\end{matrix}\right)$$ 到此我们得到了用矩阵来传播误差的算法： $$error_{hidden}=W_{hidden\rightarrow output}^T\cdot error_{output}$$

---

到此，我们已经做了大量的工作了。我们计算出了所有层的误差，接下来的工作就是根据误差来调整链接权重了。