感知机与逻辑门的实现

感知机

---

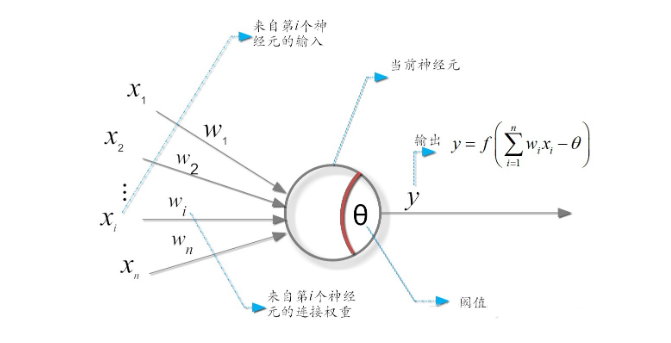
 感知机（Perceptron）由两层神经元组成，输入层接收外界信号后传递给输出层，输出层是M-P神经元（如下图），亦称” 阙值逻辑单元（threshold logic unit）“。

逻辑门的实现

---

 感知机能容易地实现逻辑与、或、非、异或运算。注意到$y=f(\sum_{i}{w_ix_i-\theta})$,假定$f$为阶跃函数:

$$sgn(x) = \begin{cases} 1, & x>= 0 \\\\ 0, & x<0 \end{cases}$$

则有：

• 与门（$ x_1\land x_2 $）：令$w_1=w_2=1,\theta=1.5$,则$y=f(1\cdot x_1+1\cdot x_2-2)$,仅当$x_1=x_2=1$时，$y=1$

# python实现与门
def AND(x1,x2):
    
    w1,w2,theta = 1.0,1.0,1.5
    result = w1*x1 + w2*x2 - theta
    if result >= 0:
        return 1
    else:
        return 0

• 或门（$x_1\lor x_2$）：令$w_1=w_2=1,\theta=0.5$,则$y=f(1\cdot x_1+1\cdot x_2-0.5)$,仅当$x_1=1$或$x_2=1$时，$y=1$。

  # python实现或门
  def OR(x1,x2):
      w1,w2,theta = 1.0,1.0,0.5
      result = w1*x1 + w2*x2 - theta
      if result >= 0:
          return 1
      else:
          return 0

• 非门（$\lnot x_1$）：令$w_1=-0.6$,$w_2=0,\theta=-0.5$,则$y=f(-0.6\cdot x_1+0\cdot x_2+0.5)$,仅当$x_1=1$时，$y=0$；当$x_1=0$时，$y=1$。

  # python 实现非门
  def NOT(x1):
      w1, theta = -0.6, -0.5
      result = w1*x1 - theta
      if result >= 0:
          return 1
      else:
          return 0

• 与非门：令$w_1=w_2=-1,\theta=-1.5$,则$y=f(1\cdot x_1+1\cdot x_2+1.5)$,仅当$x_1=x_2=1$时，$y=0$

  # python 实现与非门
  def NAND(x1,x2):
      w1,w2,theta = -1.0,-1.0,-1.5
      result = w1*x1 + w2*x2 - theta
      if result >= 0:
          return 1
      else:
          return 0

• 异或门（$x_1\oplus x_2$）：异或门在生活中有很多用处，我们常常听到下面这句话：“这件事要么你来做，要么我来做”。意思是这件事只能由我们之间的任何一个人来做，其他都不行。又比如你房间中的灯的开关一般门口一个床头一个，这样子你每按下其中任何一个开关都只会有两种结果（变得与另一个一样，变得与另一个不一样）利用这两种结果就可以构成灯的开与关。

# python 实现异或门
def ExOR(x1,x2):
    return AND(OR(x1,x2),NAND(x1,x2))